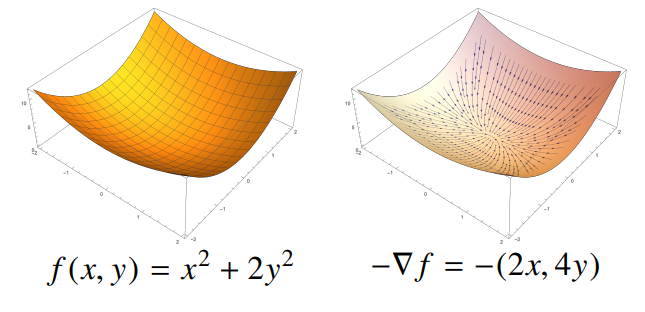[DAY 7] Gradient Descent - Easy
미분
- 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구
- 최적화에서 가장 많이 사용
- 미분(differentiation): 변화율의 극한(limit)으로 정의
- $\large{ f^\prime(x)=\lim_{h \to 0} { { f(x+h)-f(x) } \over {h}} }$
미분 코드
1 2 3 4 5 6
import sympy as sym # symbolic python from sympy.abc import x sym.diff(sym.poly(x**2 + 2*x + 3), x) # (미분대상함수, x로 미분) # Poly(2*x + 2, domain='zz')
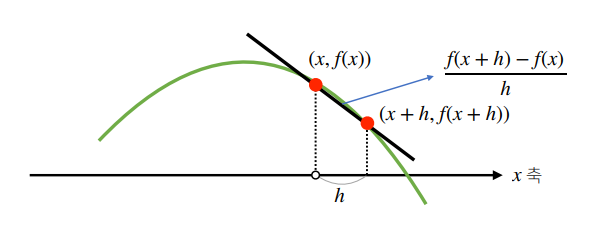
- 미분은 함수 $f$에서 주어진 점$(x, f(x))$에서의 접선의 기울기를 구함
- 아래 함수에서 $h$를 $0$으로 보내면 $({ { f(x+h)-f(x) } \over h })$에서 접선의 기울기로 수렴 (기울기/변화율의 극한)

- 아래 함수에서 $h$를 $0$으로 보내면 $({ { f(x+h)-f(x) } \over h })$에서 접선의 기울기로 수렴 (기울기/변화율의 극한)
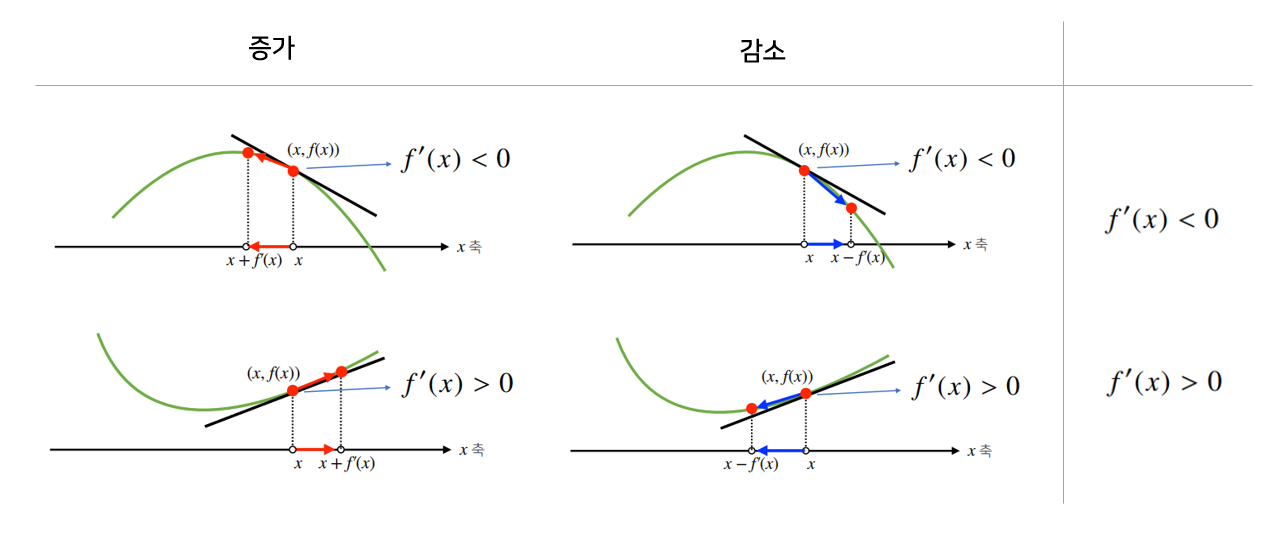
- 한 점에서 접선의 기울기를 알면, 점을 어느 방향으로 움직여야 함수값이 증가/감소하는지 알 수 있음
- 극 값에 도달하면 움직임을 멈춤
- 극값에서의 미분값: $0$ 이므로 더이상 없데이트 X
- 따라서 목적함수 최적화가 자동으로 끝남
- 양수든, 음수든, 빼주면 함수를 감소시는 방향으로 움직임 (음수를 빼는 것은 양수를 더하는 것과 같음)
경사상승법: 증가 ➡ 미분값을 더함 $x+f^\prime(x) < x$경사하강법: 감소 ➡ 미분값을 뺌 $x-f^\prime(x) > x$
- 극 값에 도달하면 움직임을 멈춤
경사상승법
- Gradient Ascent
- $x+f^\prime(x) < x$
- 미분값을 더한것 ➡ 증가방향으로 움직임
- 극대값의 위치를 구할 때 사용
- 목적함수를 최대화할 때 사용
경사하강법
- Gradient Descent
- $x-f^\prime(x) > x$
- 미분값을 뺀 것 ➡ 감소방향으로 움직임
- 극소값의 위치를 구할 때 사용
- 목적함수를 최소화할 때 사용
경사하강법(2차원)
알고리즘
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
# Input: gradient, init, lr, eps # Output: var """ gradient: 미분을 계산하는 함수 init: 시작점 lr: 학습률 eps: 알고리즘 종료조건 """ var = init grad = gradient(var) while(abs(grad) > eps): # code_1 var = var - lr * grad # code_2 grad = gradient(var) # code_3
code_1- 컴퓨터 계산시, 미분이 정확히 $0$이 되는 것은 불가능하므로 ➡
eps보다 작을 때 종료하는 조건 필요
- 컴퓨터 계산시, 미분이 정확히 $0$이 되는 것은 불가능하므로 ➡
code_2- $x-\lambda f^\prime(x)$을 계산하는 부분
lr은 학습률로서 미분을 통해 업데이트하는 속도를 조절- 학습률 조절로서 빠르거나 느리게 학습 속도 조절가능 But 매우 조심히 다뤄야함
code_3- 종료조건이 성립하기 전까지 미분값을 계속 업데이트
- 경사하강법으로 최소점을 찾는 코드
- 함수: $f(x)=x^2+2x+3$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
def func(val): fun = sym.poly(x**2 + 2*x + 3) return fun.subs(x, val), fun def func_gradient(fun, val): _, function = fun(val) diff = sym.diff(function, x) return diff.subs(x, val), diff def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5): cnt=0 val = init_point diff, _ = func_gradient(fun, init_point) while np.abs(diff) > epsilon: val = val - lr_rate*diff dif, _ = func_gradient(fun, val) cnt+=1 print("함수: {}, 연산횟수: {}, 최소점: ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0])) gradient_descent(fun=func, init_point=np.random.uniform(-2, 2))
그레디언트 벡터(Gradient Vector)
- 미분은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구 ➡ 최적화위해 사용
- 2차원 평면 위에서 $+$와 $-$ 방향을 정했던 때와 달리, 벡터의 경우는 이동방향이 다양함 ➡ 특정 좌표축에 대해 어디로 이동할지 정해야함 ➡ 편미분 사용
- 벡터가 입력인 다변수 함수의 경우, 편미분(partial differentiation)을 사용
$x$에 대해 편미분: $y$를 상수취급하고 $x$에 대해서 미분한 것
$\Large{\partial_{x_i} f(x) = lim_{h \to 0} {f(x+he_i)-f(x)} \over {h}}$
▪ $e_i$: $x$의 $i$번째 벡터(방향)에만 영향을 주는 단위벡터
▪ $i$번째 값만 1이고 나머지는 0인 단위벡터- 각 변수별로 편미분을 계산한 gradient vector을 이용하여 경사하강/경사상승법에 적용가능
- gradient vector를 사용하면, D-차원에서의 경사상승/하강법 가능
gradient descent: $-\triangledown f$
- 각 점$(x, y, z)$공간에서 $f(x, y)$표면을 따라 $-\triangledown f$ 벡터를 그렸을 때,

- 이 공간의 어디에 있든, 화살표를 따라가면 가장 빠르게 최소점에 도달가능
- $-\triangledown f(x, y)$는 각 점(x, y)에서 가장 빨리 감소하는 방향으로 흐름
- $-\triangledown f = \triangledown (-f)$
gradient ascent: $\triangledown f$
- $\triangledown f(x, y)$는 각 점(x, y)에서 가장 빨리 증가하는 방향으로 흐름
경사하강법(다차원벡터)
알고리즘
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
# Input: gradient, init, lr, eps # Output: var """ gradient: 그레디언트 벡터를 계산하는 함수 init: 시작점 lr: 학습률 eps: 알고리즘 종료조건 """ var = init grad = gradient(var) while(norm(grad) > eps): # code_1 var = var - lr * grad # code_2 grad = gradient(var) # code_3
- 경사하강법 알고리즘은 2차원의 경사하강법 알고리즘이 그대로 적용됨
- 그러나 벡터는 절대값 대신 노름(norm)을 계산해서 종료조건을 설정
경사하강법 알고리즘: 함수의 극소,극대점을 구하는데 사용되는 최적화 알고리즘