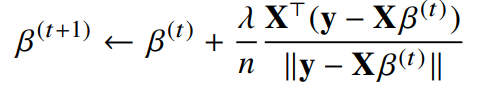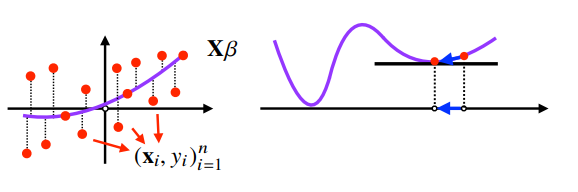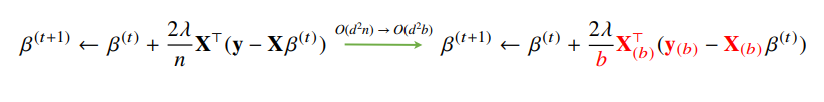[DAY 7] Gradient Descent - Hard
선형회귀 복습
- 선형회귀: n개의 데이터로 이루어진 상황에서 데이터를 가장 잘 표현하는 모델을 찾는 것
- 무어-펜로즈: 정답에 근사한 값을 사용해서, 선형모델의 계수를 쉽게 찾을 수 있음
- 경사하강법
- sklearn linear regression 라이브러리
np.linalg.pinv를 이용하여 선형모델(linear model)로 해석하는 선형회귀식을 찾을 수 있음
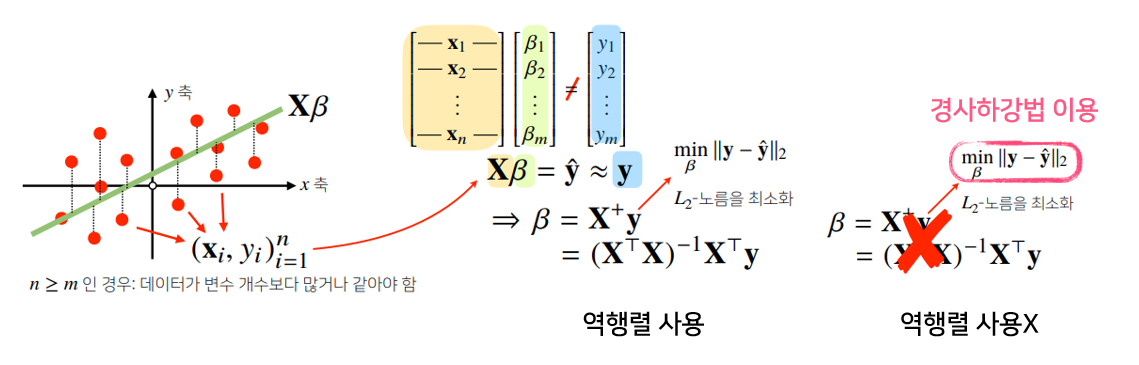
선형모델(회귀식) 찾기
- 선형모델의 경우, 역행렬을 이용하여 회귀분석이 가능
- 역행렬을 이용하지 않고, 경사하강법 이용 가능

경사하강법으로 선형회귀 계수 구하기
- 선형회귀의 목적식: $\parallel y-X_\beta \parallel_2$ (= L2-norm)
- 선형회귀의 목적식을 최소화하는 $\beta$를 찾아야하므로 다음과 같은 그레디언트 벡터를 구하는 것이 목적임
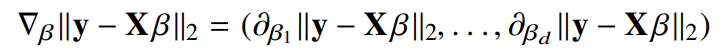
- $y$: 정답
$X_\beta$: 행렬($X$), 벡터($\beta$)
- 설명
- (두 벡터의 차이인) L2-norm을 최소화하는 $\beta$ 찾기
- $\beta$ 최소화: 목적식을 $\beta$로 미분하고 주어진 $\beta$에서 미분값을 빼면 최소값을 찾을 수 있음
- $\lVert y-X_\beta \rVert_2$ 대신 ${\lVert y-X_\beta \rVert_2}^2$를 최소화 해도 됨 (목적식 대신 목적식의 제곱)
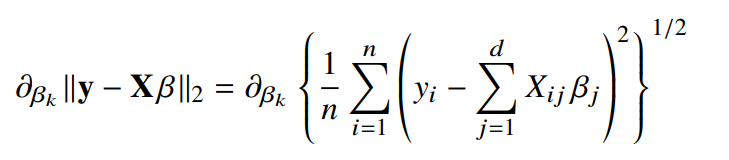
- ${1 \over n} \sum_{i=1}^n$
- $1 \over 2$ : 평균을 구하기 위해 사용
- $\sum_{i=1}^n$ : N개의 데이터를 가지고 계산한다는 의미
- $\partial_{\beta_k} \lVert y-X_\beta \rVert_2$ : 주어진 $\beta$ 벡터 내에서 $k$번째 계수에 해당하는 $\beta_k$를 사용하여 목적식을 편미분한 것
- $\sum_{j=1}^d X_{ij}$ : $N$개의 데이터를 가지고 계산
- L2-norm이므로 제곱합의 제곱근 사용
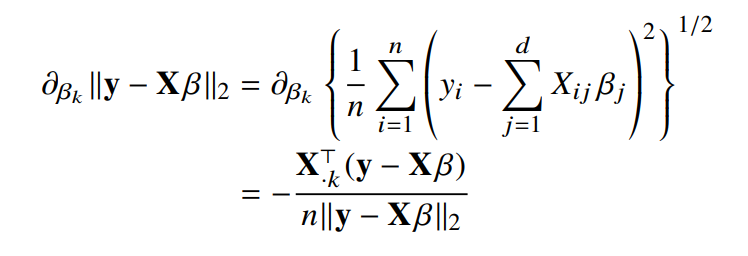
- $\partial_{\beta_k} \lVert y-X_\beta \rVert_2$의 목적식: $\lVert y-X_\beta \rVert_2$
$X_k^T$ : 행렬$X$의 $k$번째 열(column)벡터를 전치시킨 것
- 설명
- $k$번째 계수, 벡터 $k$에 대한 목적식의 편미분
- ➡ 각 요소에 대한 편미분이며, $\beta_1$ ~ $\beta_n$까지의 gradient vector 구할 수 있음
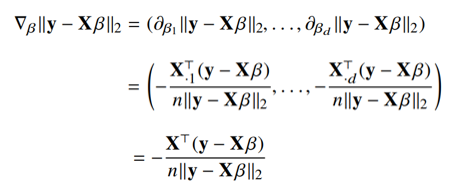
- $X_\beta$(선형모델)를 계수 $\beta$에 대해 미분한 결과인 $X^T$만 곱해진다는 것을 의미
- ➡ 이러한 점은 D차원이나 1차원이나 동일함
목적식을 최소화하는 $\beta$를 구하는 경사하강법 알고리즘
 위의 식을 풀면 다음과 같음
위의 식을 풀면 다음과 같음 
- t를 반복적으로 계산해보면 목적식을 최적화하는 $\beta$를 구할 수 있음
- 이전과정에 비해, 다변수인 것을 제외하면 모든 요소가 같음
- $\beta^{(t)}$: t번째 단계에서의 coefficient
- $\lambda$ : 학습률 - 수렴속도 지정
- $\triangledown_\beta$ : gradient vector(미분값)
- $\lambda \triangledown_\beta \lVert y-X\beta^(t) \rVert$ : gradient factor
선형회귀의 목적식은 L2-norm 과 같고, 경사하강법에서 L2-norm 대신 L2-norm의 제곱을 사용하는 것도 가능함(식이 간단해짐!) ➡ 둘은 동일한 결과를 가져옴
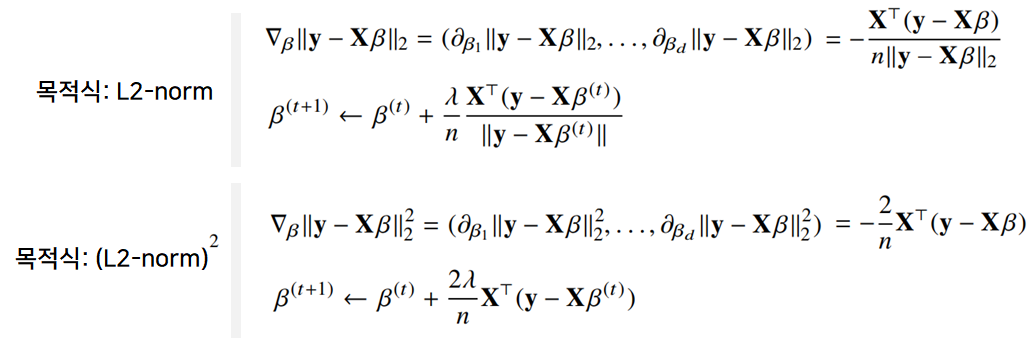
경사하강법 기반 선형회귀 알고리즘
1
2
3
4
5
6
7
8
9
10
11
# Input: X, y, lr, T
# Output: beta
"""
norm: L2-norm을 계산하는 함수
lr: 학습률
T: 학습횟수
"""
for t in range(T): # eps로 사용가능, 지정된 시간의 종료조건
error = y - X @ beta
grad = - transpose(X) @ error # @: 행렬곱
beta = beta - lr * grad
- 종료 조건을 일정 학습횟수로 변경한 점만 제외하면 앞에서 배운 경사하강법 알고리즘과 같음
error,grad,beta를 구하는 과정 : $\triangledown_\beta \lVert y-X_\beta \rVert_2^2$ 항을 계산해서 $\beta$를 업데이트하는 과정- $\beta$: 주어진 목적식을 최소화하는 선형모델의 계수
- 무어-펠로스 역행렬 없이 계수찾기 가능
- 경사하강법 알고리즘을 사용하면 역행렬을 이용하지 않고 회귀계수를 계산할 수 있음
- 경사하강법 알고리즘에서 학습률과 학습횟수는 중요한 hyperparameter
- 학습률(
lr)이 너무 작을 경우 ➡ 수렴이 늦어짐 - 학습률이 너무 클 경우 ➡ 불안정한 gradient 움직임이 발생함
- 학습률(
Convex Function (볼록함수)
- 이론적으로, 경사하강법은 미분가능하고 볼록한 함수에 대하여, 적절한 학습률과 학습횟수를 선택했을 때, 수렴이 보장되어 있음
- 볼록한 함수는 그레디언트 벡터가 항상 최소점을 향함
- 특히 선형회귀의 경우, 목적식 $\lVert y-X_\beta \rVert_2$은 회귀계수 $\beta$에 대해 볼록함수이기 때문에 알고리즘을 충분히 돌리면 수렴이 보장됨

- 그러나 비선형회귀 문제의 경우, 목적식이 볼록하지 않을 수 있으므로 수렴이 항상 보장되지는 않음
- 특히 딥러닝을 사용하는 경우, 목적식은 대부분 볼록함수가 아님(non-convex function, 볼록성 보장X)

- 특히 딥러닝을 사용하는 경우, 목적식은 대부분 볼록함수가 아님(non-convex function, 볼록성 보장X)
확률적 경사하강법
- (SGD)stochastic gradient descent
- 모든 데이터를 사용하여 업데이트하는 대신,데이터 한개 혹은 일부를 활용하여 업데이트 진행
- 데이터를 일부 활용하는 것을 mini batch라고 함
- 요즘의 SGD는 mini batch SGD를 의미하곤 함
- 볼록이 아닌(non-convex) 목적식은 SGD를 통해 최적화 가능
- 언제나 성립하는 것은 아니지만, 딥러닝의 경우, SGD가 경사하강법보다 실증적으로 더 낫다고 검증되었음
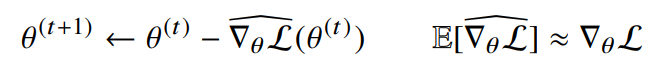
- $E$: Expectation, 무한시행 시에서의 평균값
- $\widehat{\triangledown_\theta\mathcal{L}}(\theta^{t})$ : stocastic 추정치
- $\triangledown_\theta\mathcal{L}$ : gradient
- SGD는 데이터의 일부를 가지고 파라미터를 업데이트하기 때문에 연산자원을 좀 더 효율적으로 활용하여 파라미터 최적화 가능

- 전체데이터 $(X, y)$를쓰지않고미니배치$(X_{(b)}, y_{(b)})$를 써서 업데이트하므로 연산량이 $b \over n$로 감소함
- $O(d^2n)$ ➡ $O(d^2b)$ (※ n:데이터 양, $O()$: 연산량)
- 전체데이터 $(X, y)$를쓰지않고미니배치$(X_{(b)}, y_{(b)})$를 써서 업데이트하므로 연산량이 $b \over n$로 감소함
미니배치 연산

기존 경사하강법
- 경사하강법은 전체 데이터 $\mathcal{D}=(X, y)$를 가지고 목적식($\mathcal{L}$)의 그레디언트 벡터인 $\large{ \triangledown_\theta\mathcal{L}(\mathcal{D}, \theta) }$를 계산
- $\triangledown_\theta$ : gradient
- $\mathcal{L}$ : 목적식
- $\mathcal{D}, \theta$ : 나블라, 세타
- $\mathcal{L}(\mathcal{D}, \theta)$ : 전체 데이터 $\mathcal{D}$와 파라미터 $\theta$로 측정된 목적식
- 주어진 파라미터 $\theta$에서 주어진 목적값에 최소점으로 향하는 방향 안내
SGD
- SGD는 미니배치 $\mathcal{D}{(b)} = (X{(b)}, y_{(b)}) \subset \mathcal{D}$를 가지고 그레디언트 벡터를 계산
- 미니배치는 전체 데이터를 사용하는 결과와 같지는 않겠지만 유사하게 나올것임
- 미니배치 $\mathcal{D}_{(b)}$를 가지고 목적식의 그레디언트를 근사해서 계산
- SGD는 mini batch를 사용하여 매번 mini batch samling 할때마다 목적식의 모양이 변화함
- 매번 다른 미니배치를 사용하기 때문에 곡선 모양이 바뀌게 됨
- 목적식이 조금 바뀌지만 방향은 옳은 방향일 것이라 추측
- (↔ 경사하강법은 t step을 순차적으로 진행)
- 극소,극대점에서의 gradient vector가 0 벡터가 되더라도, 실제로는 함수 전체의 극소/극대점이 아닐 수 있음 ➡ 기울기를 변형하여 local minima 탈출 가능
- local minimum 문제를 어느정도 해소할 수 있음(기울기가 0 벡터인 경우의 목적식이 변경되므로!)
- 이 특징을 이용하여 non-convex function에서도 최대/최소점을 찾을 수 있음
- SGD는 볼록이 아닌 목적식에서도 사용가능하므로 경사하강법보다 머신러닝 학습에 더 효율적
- 학습률, 학습횟수, 미니배치 사이즈 고려 필요
- 너무 작은 미니배치는 일반 경사하강법보다 느린 수렴을 일으킴

- 너무 작은 미니배치는 일반 경사하강법보다 느린 수렴을 일으킴
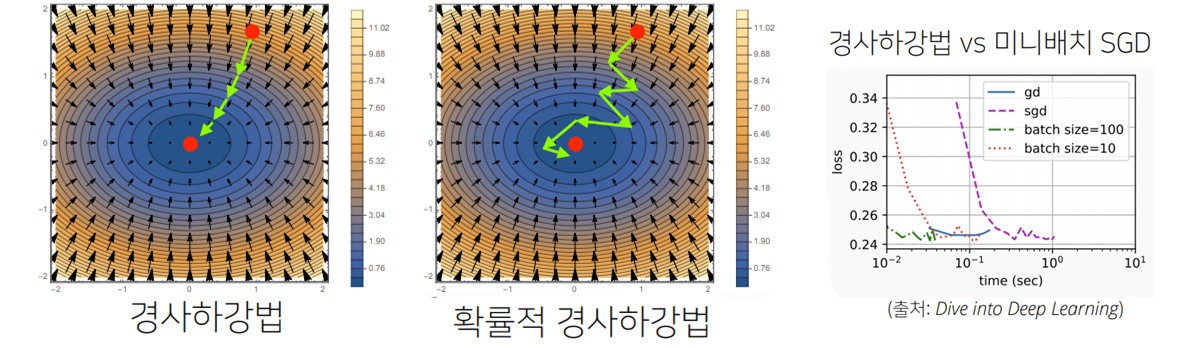
- SGD는 일직선으로 움직이지는 않지만, 최소점으로 향하는 움직임을 보이는 성질은 경사하강법과 동일
- 돌아서 가는 것처럼 보이지만 실제로는 더 적은 데이터를 계산하는 것이므로, 움직임(화살표)의 속도가 더 빠름 ➡ 일반 경사하강법보다 빠름! (그림3-수렴속도 비교 확인)
- 만일 일반적인 경사하강법처럼 모든 데이터를 업로드하면 메모리가 부족하여 out-of-memory가 발생
- 반면에 미니배치로 쪼갠 데이터를 사용하면 빠르게 연산이 가능하며 하드웨어적인 메모리 부족 한계를 해결할 수 있음
GPU에서 행렬연산과 모델 파라미터를 업데이트하는 동안 CPU는 전처리와 GPU에서 업로드할 데이터를 준비함- 알고리즘의 효율성과 하드웨어를 고려하면 SGD는 필수!

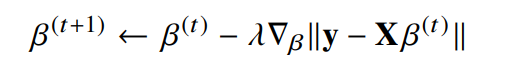 위의 식을 풀면 다음과 같음
위의 식을 풀면 다음과 같음