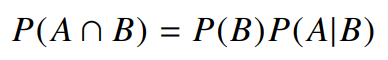[DAY 11] 베이즈 통계학
조건부확률

조건부확률 $P(A B)$ - 사건 $B$가 일어난 상황에서 사건 $A$가 발생할 확률
- $P(A \cap B)$가 일어날 확률 / 특정사건 $B$가 일어날 확률
- P, A given B
- $P(A \cap B)$
- 사건 $A$와 사건 $B$가 동시에 일어날 경우
베이즈정리
- 두 확률변수의 사전확률-사후확률 간 사이의 관계를 정리
- 데이터가 새로 추가될 때 정보를 업데이트하는 기법
- sample space가 변하기 때문에 필요
- $P(B)$의 sample space : 전체집합
$P(A B)$의 sample space : $P(B)$
- 모수 추정 시에 사용하게 됨
- 조건부확률을 이용하여 정보를 갱신하는 방법을 알려줌
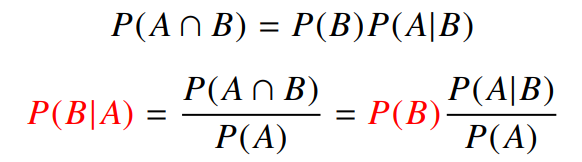
$A$라는 새로운 정보가 주어졌을 때 $P(B)$로 부터 $P(A B)$를 계산하는 방법을 제공 ➡ 베이즈 정리

- 사후확률(posterior)
- 데이터 관측 시, 이 파라미터가 성립할 확률
- 데이터 관측 이후에 측정하는 값
- 사전확률(prior)
- 데이터가 주어지지 않았을 때, $\theta$에 대한 모델링 이전에 사전에 주어진 확률
- 데이터 분석 전, 모수나 가설 등… 도엘링 하고자 하는 타겟데 애해서 사전에 가설을 깔아두고, 확률분포를 설정하는 것
- 베이즈 정리를 통해서 이 확률분포를 업데이트 하게 됨
- 증거(evidence)
- 데이터 전체의 분포
- 가능도(likelihood)
- 현재 주어진 모수(파라미터, 가정)에서 이 데이터가 관찰될 확률
- $\theta$: 가설, hypuothesis
- 모델링하는 이벤트
- 모델에서 계산하고자 하는 파라미터(모수)
- $\mathcal{D}$: 새로 관찰할 데이터
예제1
- COVID-99의 발병률이 10%로 알려져있음
- COVID-99에 실제로 걸렸을 때, 검진될 확률은 99% 이고, 실제로 걸리지 않았을 때, 오검진될 확률이 1% 라고 함
- 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때, 정말로 COVID-99에 감염되었을 확률은?

$\theta$ : COVID-99 발병 사건으로 정의 ➡ (관찰불가) $\mathcal{D}$ : 테스트 결과라고 정의 ➡ (관찰가능) 만일 $P(\mathcal{D} | \neg \theta)$를 모른다면, 이 문제는 풀기 어려움
- 사전확률, 민감도(Recall), 오탐율(Falsealarm)을 가지고 정밀도(Precision)를 계산
예제2
- COVID-99의 발병률이 10%로 알려져있음
- COVID-99에 실제로 걸렸을 때, 검진될 확률은 99% 이고, 실제로 걸리지 않았을 때, 오검진될 확률이 10% 라고 함
- 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때, 정말로 COVID-99에 감염되었을 확률은?
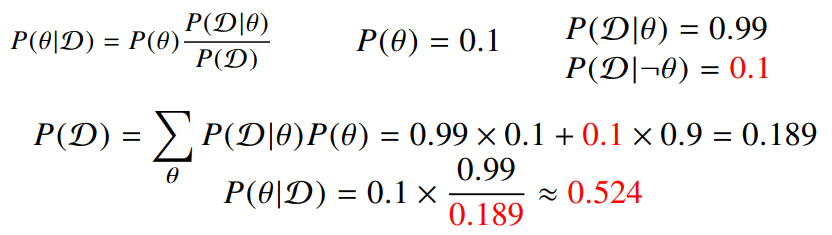
- 오탐률이 오르면, 테스트의 정밀도(precision)는 떨어짐
- 실제 걸렸을 때, 걸렸다고 분류를 잘해도, 안걸렸을 때를 걸렸다고 하면 정밀도가 떨어짐
조건부확률의 시각화
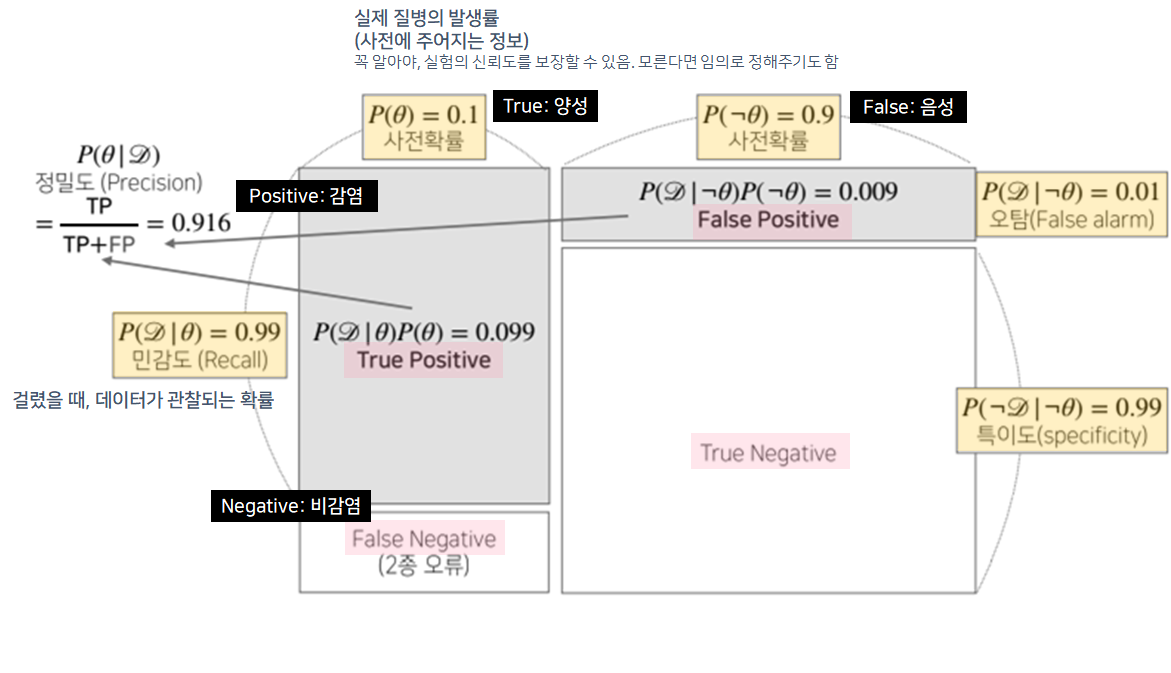
- 1종오류와 2종오류 중, 어떤 것을 줄일지가 중요함
- 2종오류의 경우, 의료분야에서 신경을 많이 써야함
- 정밀도에서 FP 혹은 TP가 분모에 들어가므로 둘 중에 하나라도 커지면 분모가 커지므로, 정밀도가 떨어지는 결과를 초래
- 가설검정, 신뢰도 측정방식
베이즈 정리를 통한 정보의 갱신
- 베이즈 정리를 통해, 새로운 데이터가 들어왔을 때, 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있음

$\theta$ : 모델의 파라미터 ➡ 점점 업데이트 하여 모델의 정확도, 예측력을 높임 $P( \theta )$: 사전확률
예제3
COVID-99 판정을 받은 사람이 두번째 검진을 받았을 때도 양성이 나왔을때 진짜 COVID-99에 걸렸을 확률은?

- 업데이트 된 정보를 통해 모델링 가능 ➡ 유효한 테스팅 가능
- 세번째 검사해도 양성이 나오면,정밀도가 99.1% 까지 갱신됨
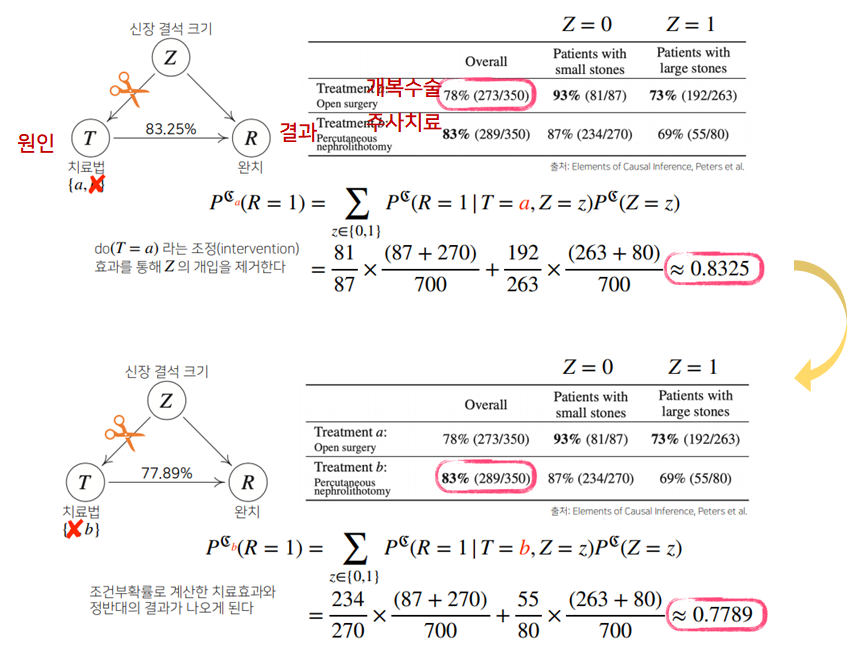
조건부확률과 인과관계
조건부 확률은 인과관계인가? NO
- 인과관계: 두개의 사건이 있을 때, A가 B의 원인인지 알아내는 것
- 조건부 확률은 유용한 통계적 해석을 제공하지만, 인과관계(causality)를 추론할 때 함부로 사용해서는 안됨
- 데이터가 많아져도 조건부 확률만 가지고 인과관계를 추론하는 것은 불가능
- 인과관계는 데이터 분포의 변화에 강건한 예측모형을 만들 때 필요
- 단, 인과관계만으로는 높은 예측 정확도를 담보하기 어려움
- 데이터 분포의 변화(데이터 유입, 새로운 정책 사용)시, 시나리오에 따라 예측확률에 큰 차이가 생김

- 인과관계 기반 예측모형은 높은 예측 정확도를 담보하지는 않음
- 그러나 데이터 분포의 변화에 강건함
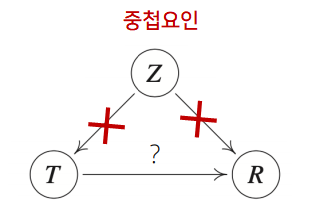
- 인과관계를 알아내기 위해서는 중첩요인(confounding factor) 의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산해야 함
- 만일 $Z$의 효과를 제거하지 않으면 가짜 연관성(spurious correlation) 이 나옴 ➡ 예측모델의 정확도를 떨어뜨리는 요인
ex) 키와 IQ의 높은 연관성의 이유? “나이”라는 중첩요소 때문! 그래서 데이터 분석에서 가짜 연관성에 의한 오류 도출 가능
심슨의 패러독스 단순히 a와 b를 통해 조건부확률로 사용하면 안됨
인과관계 추론
- 내용 추가 필요

추후에 응용확률에서 배운 베이즈정리, 베이즈 결정이론 등에 대해서 올릴 예정