[DAY 11] NN & MLP
Neural Network?
- 신경망, 뇌를 모방하고자 하는 시스템
- 함수적 접근: 이미지 분류하기 위해 벡터, 행렬곱 등의 함수를 모방하는 Function approximator 라고 보는 것
- function approximator: parameter를 이용하여 실제 값에 approximate하는 함수
- 이미지라는 텐서가 주어졌을 때, (라벨이라는 벡터가 튀어나오는 함수가 있을 때,) 그것을 내가 정의한 어떤 것으로 만드는 함수로 근사하는 모델
- affine transformation(행렬곱) (모든 선형 변환은 affine trans임)
- non-linear, activation function(비선형 연산이 반복적으로 이뤄짐)
우리가 하늘을 날고싶다고 해서 새처럼 움직일 필요는 없듯이, AI도 인간의 뇌를 모방할 필요는 없음. 시작이 모방이었을지는 모르지만, 현재의 동작방식은 인간의 뇌를 모방했다기에는 너무 달라졌음. 따라서, 뇌 구조를 따라가는 것보다 모델만 두고 수학적으로 접근하는 것이 더 맞을 것
Linear Neural Network
- linear regression의 목적: 입력이 1차원, 출력이 1차원일 때, 이 둘을 연결하는 모델을 찾는 것
- 라인에 대한 기울기와 절편, 이 두개의 파라미터를 찾는 과정
- 1차원 $x$, 1차원 $y$
- 스칼라 $w$, bias $b$
- $x$ ➡ $\hat{y}$으로 맵핑되는 선형모델을 정의하는 w와 b를 찾는 것이 목적
- loss: 우리가 이루고자하는 현상을 이루었을 때, 줄어드는 함수
- 가장 간단한, 회귀문제에서 loss function은 squared loss function을 사용할 수 있음
- $y_i$: $i$번째 데이터의 출력값
- $\hat{y_i}$: $x_i$를 집어넣었을 때, 나의 현재 모델에서 얻을 수 있는 출력값
- 데이터를 잘 설명할 수 있는 모델을 찾는 것이니까, NN의 출력값과 나의 데이터간의 차이를 줄이는 것이 목적
$W$와 $b$를 찾는 방법?
- 여러가지 방법이 존재
- Analytic Function(해석함수) 존재: 바로 w와 b 를 찾을 수 있음(loss를 최소화하는)
- 해석함수: 국소적으로(locally) 수렴하는 멱급수로 나타낼 수 있는 함수
- 목적: loss를 줄이는 것 ➡ 내 파라미터가 어느 방향으로 움직여야 loss function이 줄어드는지를 찾고, 그 방향으로 파라미터를 바꾸면 됨
- loss를 내 파라미터로 각각 미분하는 방향의 음수 방향으로 업데이트
- Then, (loss를 최소화하는) 파라미터를 최적화 할 수 있음
n개의 데이터를 모두 활용했을 때, 학습데이터의 target data와 (model의 output)output의 제곱을 minimize하는 loss func의 w에 대한 편미분
$W$에, 이 편미분 값에 적절한 값을 곱해서 빼주면 됨
✔ Gradient Descent 방법이라고 부름
loss를 편미분한 것을 빼주기 때문에 gradient descent라고 부르고,
reward 같이, 편미분 한 것을 더해주는 경우에는 gradient ascent라고 부름
용어
- Neural Network: 단순히 선형만 있는 것이 아니라, 비선형이 포함
- Deep Learning: 여러 레이어가 쌓인것
- back propagation: 마지막 최종단에서 나온 loss function을 전체 파라미터로 모두 미분하는 것
- Gradient Descent: backpropagation으로 나오는 각 파라미터만의 편미분을 업데이트 시키는 것
✔ step size 설정은 중요함 ✔
step size가 너무 크면 학습이 잘 안됨
왜냐하면) gradient 정보는 굉장히 local한 정보이므로
바로 그 위치에서 조금밖에 유효하지 않기 때문에 적절한 step size를 찾는 것이 중요
자신의 근처에서만 유효한 성질을 가짐
- Adaptive Learning Rate: step size를 자동으로 바꿔주는 것
모델의 표현
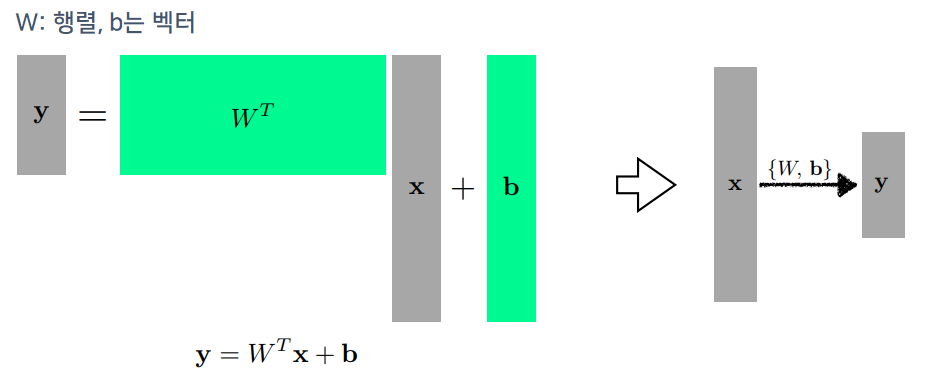
- Affine Transform: 행렬을 사용하여 모델을 N ➡ M차원으로 transform 가능, mapping
NN을 깊게 쌓는다면?

왼쪽의 식(여러 linear의 행렬곱)은 결국 한단짜리 NN과 다를 게 없음
그래서 중간에 non-linear transform 필요
➡ 네트워크의 표현력을 늘리기 위해서
단순히 선형결합을 N번 반복하는 것이 아닌, 한번 선형결합이 반복되는 경우, activation function을 곱해서(sigmoid, tanh, relu…) non-linear transform을 거치고, 그렇게 얻어지는 feature vector를 다시 선형변환하고, non-linear transform 거치고… 이와 같은 형식을 N번 반복하게 되면, 더 많은 표현력을 가질 수 있음
➡ 이러한 방식으로 구성된 것이 NN이라고 할 수 있음
Activation Function
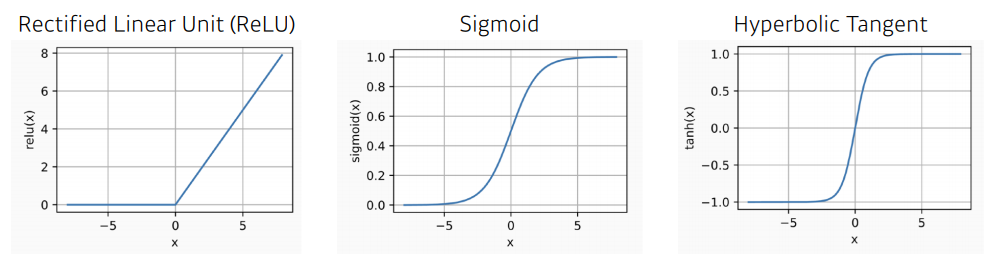
- ReLU: output이 있으면, 0 이하는 0으로 두고, 0 이상은 가져가겠음
- Sigmoid: 출력값을 항상 0~1사이의 값으로 제한하겠음
- 모든 activation function은 ✔ Non-linear Function이어야 의미가 있음!
Universal Approximation Theorem
- hidden network가 하나 있는 NN은 어떤 대부분의 연속적인 measureable function을 근사할 수 있음(우리가 원하는, 근사하고 싶은 정도까지)
- ➡ hidden layer가 한개만 있는 네트워크의 표현력은 우리가 일반적으로 생각할 수 있는 continuous function을 모두 포함 ➡ 그래서 NN 결과가 좋은것임!
- 그러나 이것은 존재성만을 보인것
- 이런것을 만족하는 NN이 세상 어디에 존재한다는 것이고, 내가 학습한 NN이 그 성질을 만족할 것이라고 할 수 는 없음
- ✔ 결론: NN의 표현력이 굉장히 큼(그러나 어떻게 찾는지는 모름)
Multi-Layer Perceptron
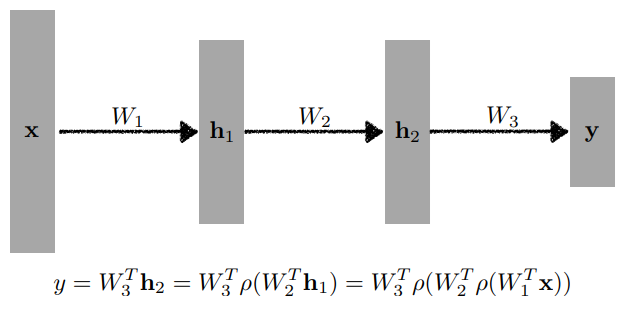
- 입력이 주어져있고, linear과 non-linear를 거쳐서 나온 hidden vector가 있고, 히든 레이어에서 다시 Affine Transformation 그리고 non-linear(없을수도 있음)
- 이렇게 만들어진 히든레이어가 있는 두 레이어의 신경망을 MLP라고 부름
- 물론 이걸 더 깊게 만들수도 있음
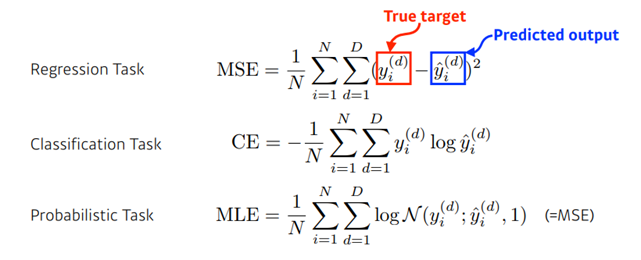
- Cross Entropy, CE
- 분류문제의 output은 원핫벡터로 표현
- 내가 찾고자하는 벡터가 10차원이면 NN에서 10차원의 벡터가 나오게 됨
- 결국, y는, 하나만 1이고, 나머지는 0인 벡터
- 그러면 Cross Entropy를 최소화한다는 것이 무슨말이냐면, 내 뉴럴넷의 출력값 중에서, 적절한 클래스에 해당한 값만 높이겠다는 것(그 차원에 해당하는 출력값을 키우겠다는 말)
- 분류를 한다는 것은, 출력중에 가장 큰 값이 들어가있는 인덱스만을 고려하게 됨 ➡ 그 값이 얼마나 큰지는 별로 중요하지않고, 다른 값들에 비해서 높기만 하면 됨
- 근데 이걸 수학적으로 표현하는 것이 까다로우니까, 분류문제에서는 Cross Entropy를 사용하게 되는 것임
- 이제 Cross Entropy가 분류 문제를 푸는데 최적일까를 생각해볼 수 있음
- MSE
- loss를 줄이고자 함
- 근데 이게 항상우리의 목적을 완성하지는 않음
- ➡ 사실 제곱도 가능하고 절댓값도 가능함
- 근데 loss func을 다르게 썼을 때, 성질이 달라짐
- 왜냐면, 어떤 outlier가 있을 때, (에러가 많이 낀 학습데이터가 있을 때)
- 큰 target data의 오류가 끼게 되면, 그 데이터를 맞추려다가 전반적인 NN이 망가지게 됨
- 그래서 MSE는, 언제나 우리가 원하는 func을 찾는데 항상 도움이 되지는 않음
- 그래서 loss가 어떤 성질을 가지는지, 이게 왜 내가 원하는 결과를 얻어내는지 확인을 꼭 해야함
- Probabilistic Task
- 내 모델이, 단순히 어떤 출력값의 숫자가 아니라 확률적인 모델로 만들고싶을 때
- 단순히 어떤 분류로 나누는 것이 아닌, 어떤 confidence정보, uncertainty를 찾고싶은 경우
- 가우시안의 log likelihood를 maximize
