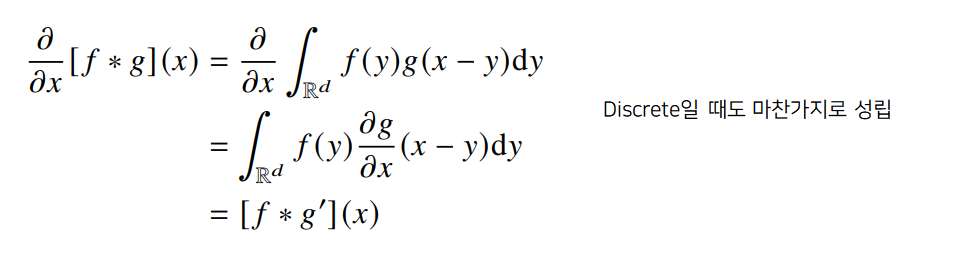[DAY 11] Convolutional Neural Network (CNN)
Convolution 연산
MLP
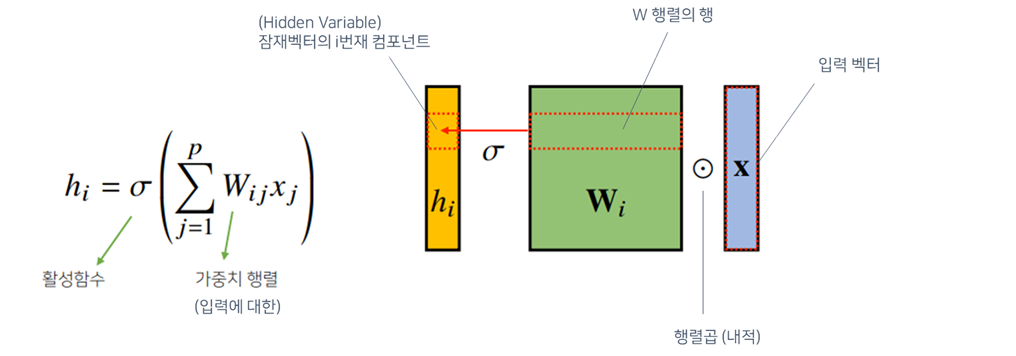
- 지금까지 배운 다층신경망(MLP)은 각 뉴런들 선형모델과 활성함수로 모두 연결된(fullyconnected) 구조
- 각 성분 $h_i$에 대응하는 가중치 행 $W_i$이 필요
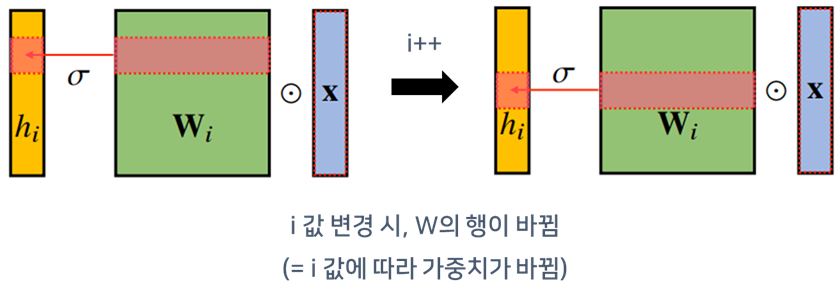
- $i$가 바뀌면, 사용되는 가중치도 바뀜
- 가중치 행렬, 찾아야하는 파라미터가 큼
Convolution 연산
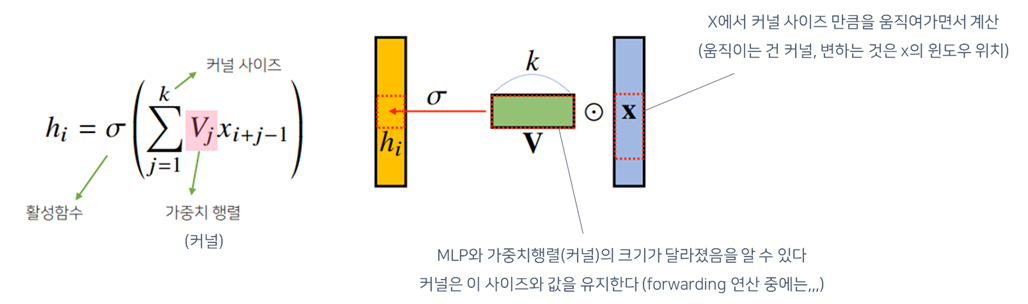
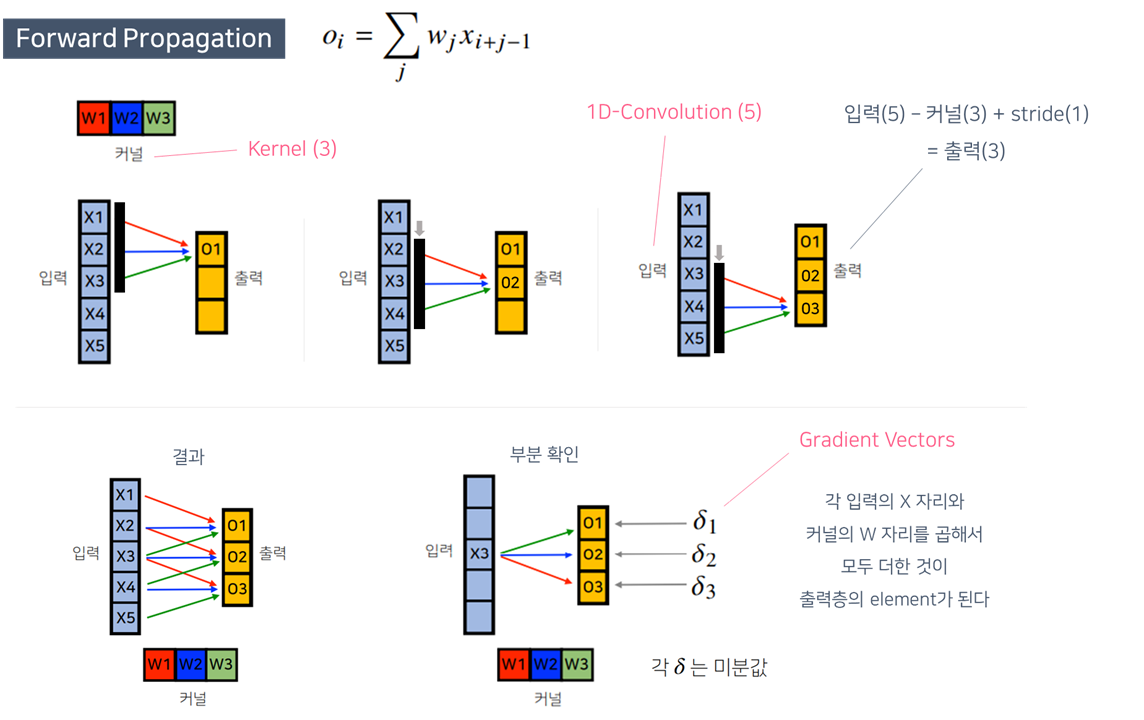
- Convolution연산은 MLP와 달리 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조
- MLP와 다르게, 커널이라는 고정된 가중치 행렬을 사용 (가중치행렬 = 커널)
- 커널도 결국 선형변환의 한 종류임
- 대신, 가중치 행렬이 $i$에 따라 바뀌지 않고 고정되어있음 ➡ 파라미터 사이즈를 줄일 수 있음!
- 고정된 가중치 행렬을 이동시켜가며 연산
- 모든 $i$에 대해 적용되는 커널은 $V$로 같고, 커널의 사이즈만큼 입력벡터 $x$상에서 이동하면서 적용함
- ➡ MLP와 다른점!
- 활성화 함수를 제외한 Convolution 연산은 선형변환
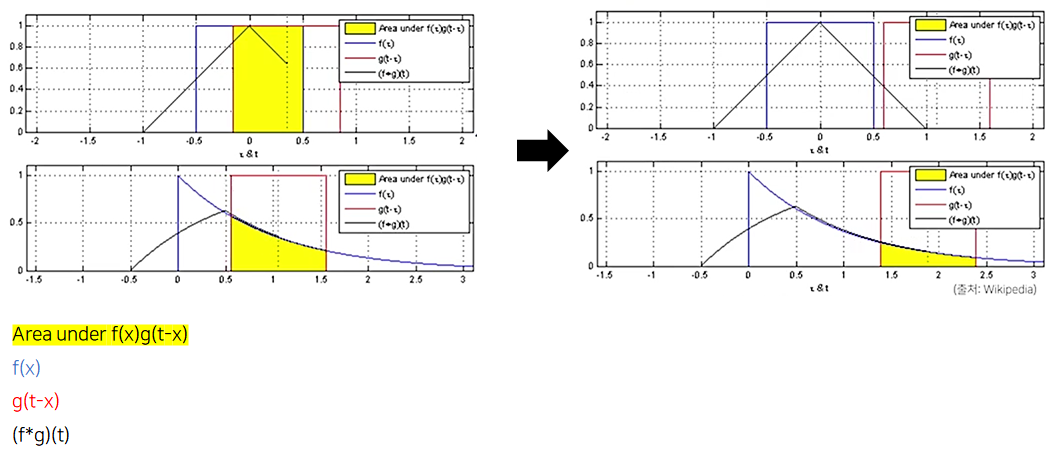
- Convolution연산의 수학적인 의미는 신호(signal)를 커널을 이용해 국소적(local)으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링하는 것
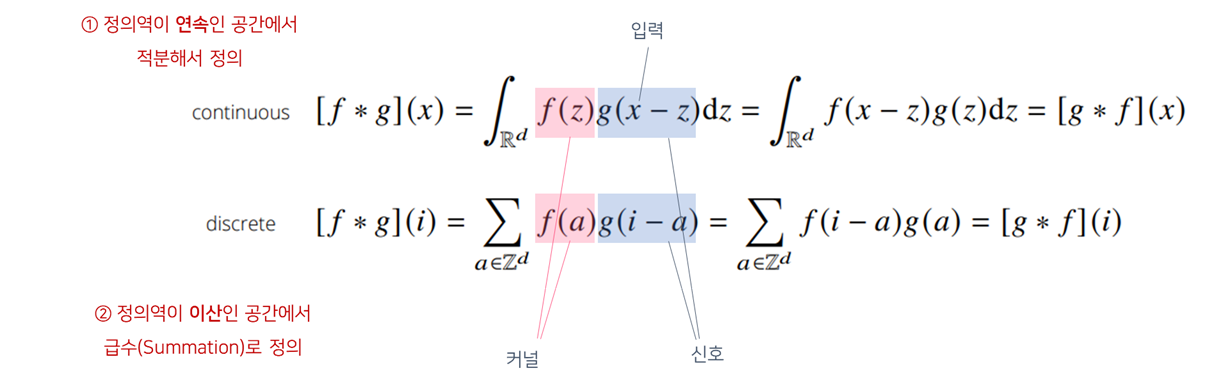
- 전체 정의역에서 $f, g$를 각각 $z$를 움직여가며 두 함수를 곱해주고, 적분
- 위의 식은 아래와 같이 바꿔어 쓸 수 있는데, 전체공간에서 볼때는 $\pm$ 기호는 별로 중요하지 않음
CNN에서 사용하는 연산은 사실 convolution이 아니고 cross-correlation(덧셈) 연산이지만, 예전부터 Convolution이라 불러왔으니 CNN이라고 써도 됨
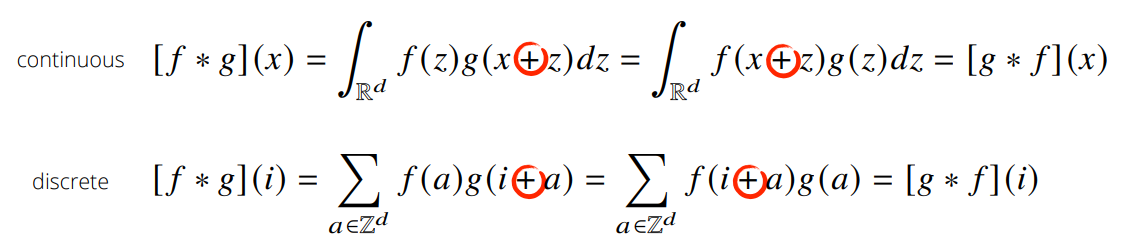
- 커널은 정의역 내에서 움직여도 변하지 않고(translation invariant) 주어진 신호에 국소적(local)으로 적용(= “locality가 있다”)
- 커널은 입력의 각 부분에 대해 공통적으로 사용됨(변하지 않는 특성을 가짐)
- 영상의 우측에 고양이가 있던지 왼쪽에 고양이가 있던지, 그것을 고양이로 분류해 낸다는 것
영상처리에서 Convolution convolution 연산은 영상처리에서 많이 사용 커널의 종류에 따라 다양한 영상처리 가능 ex) 노이즈 제거, 블러, …
다양한 차원에서의 Convolution
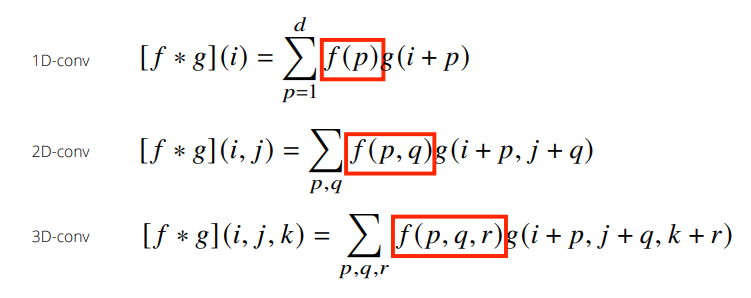
$i, j, k$가 바뀌어도 커널 $f$의 값은 바뀌지 않음(➡ 위치에 따라 값이 변경되지 않음)
- Convolution 연산은 1차원 뿐만 아니라 다양한 차원에서 계산 가능
- 1D-conv: 한 변수에 대해 움직임(이전 슬라이드들)
- 2D-conv: 두 개의 밑을 가짐(두 개의 좌표계에 동시에 움직이며 적용됨)
- 3D-conv: 세 개의 밑을 가짐(세 개의 좌표계에 동시에 움직이며 적용됨)
- 데이터의 성격에 따라 사용하는 커널이 달라짐
- 1D-conv: 음성, 텍스트, …(1D)
- 2D-conv: 흑백 이미지
- 3D-conv: 컬러 이미지
- 영상 ➡ CNN 많이 사용
2차원 Convolution 연산
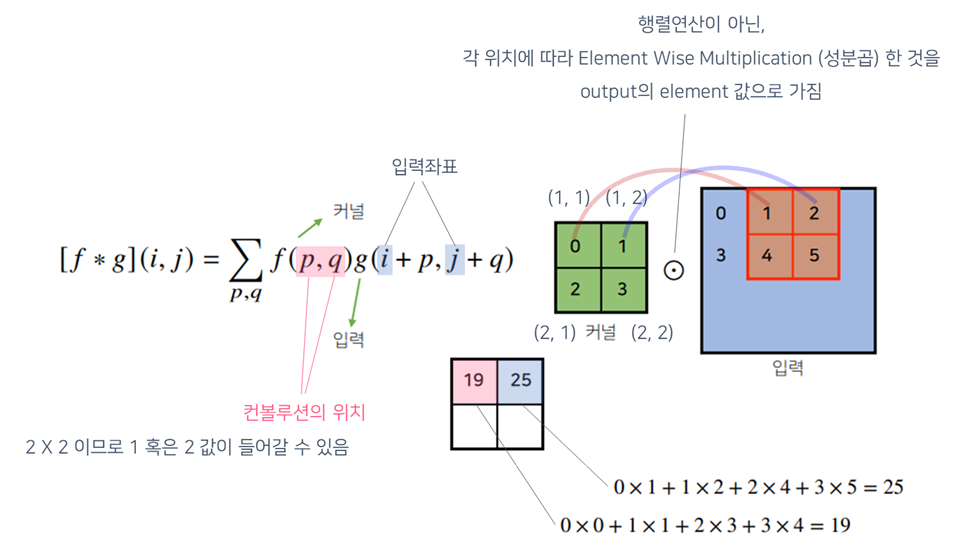
- 2D-Conv 연산은 이와달리 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조
- 1차원은 입력벡터에서 커널을 이동시킴
- 2차원은 입력행렬에 해당하는 데이터에서, 커널을 $x, y$ 방향으로 한칸씩 움직여가면서 적용 ➡ 행렬모양의 커널 사용
- 커널의 크기만큼 연산
- 한번의 forward 연산하는 동안에 커널의 값은 변경되지 않고 유지됨
- 단순히 커널의 위치를 옮겨서 input값들과 계산하게 됨
- 입력과 커널사이즈를 맞춰서 계산
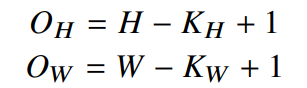
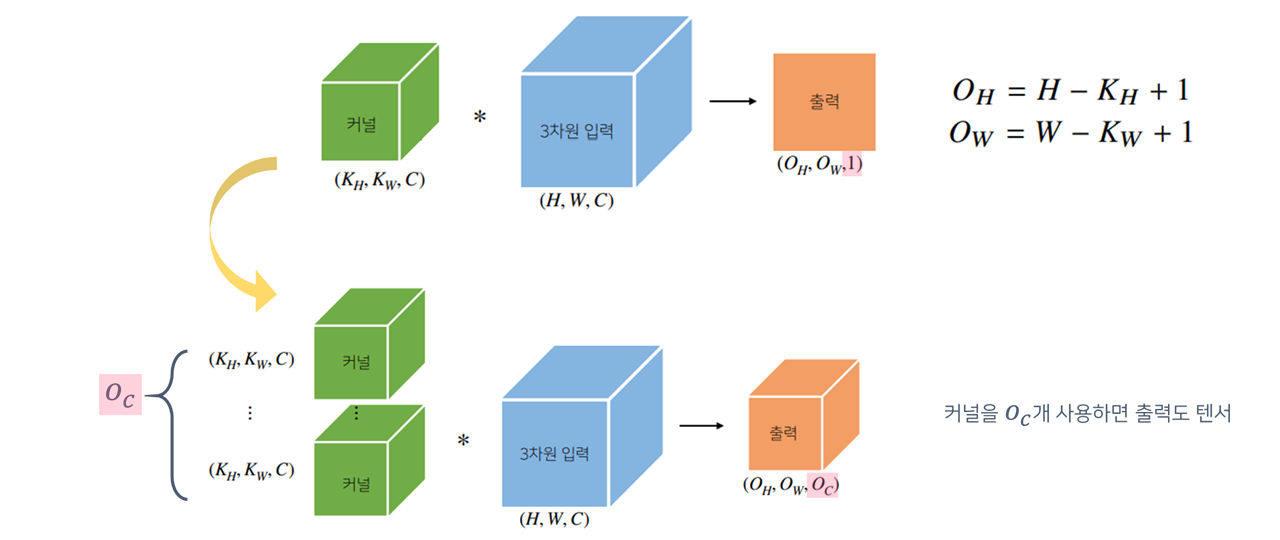
- 입력크기를 $(H, W)$, 커널크기를 $(K_H, K_W)$,출력크기를 $(O_H, O_W)$라 하면, 출력크기는 다음과 같이 계산
- 입력과 커널의 크기를 알면, 출력의 크기를 미리 에측할 수 있고
- 입력과 출력의 feature map 사이즈를 알면 파라미터의 수를 계산할 수 있음
ex) 28 x 28 입력을 3 x 3 커널로 2D-Conv 연산을 하면, 26 x 26 계산법: 입력행(28) - 커널행(3) + stride(1) = 출력행(26)
3차원 Convolution 연산
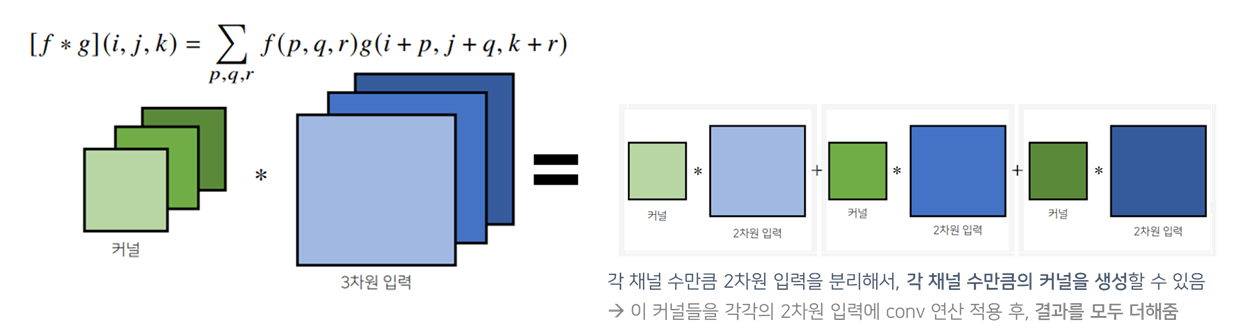
- 3차원 Convolution의 경우, 2차원 Convolution을 N번(채널수만큼 만들어서) 적용한다고 생각!
- 3차원부터는 행렬이 아닌, 텐서
- 3D-Conv 연산에서 커널의 채널수와 입력의 채널수가 같아야 함
- 텐서를 직육면체 블록으로 이해하면 좀 더 이해하기 쉬움
- ➡ 그러면 영상에서의 conv 절차를 이해하는데 도움이 될 것!
- 커널은 채널이 여러개인 텐서로 이해하기
- 3차원 입력은 2차원 입력이 여러개
- 결과적으로 채널이 1개인 출력이 도출됨
- 커널과 입력의 channel수를 같도록 설정했고, 이들은 연산 후에 모두 더해졌기 때문에 출력의 차원이 1
- 가로($O_H$), 세로($O_W$)는 앞서 배운 출력 차원의 계산법이 그대로 적용되었음
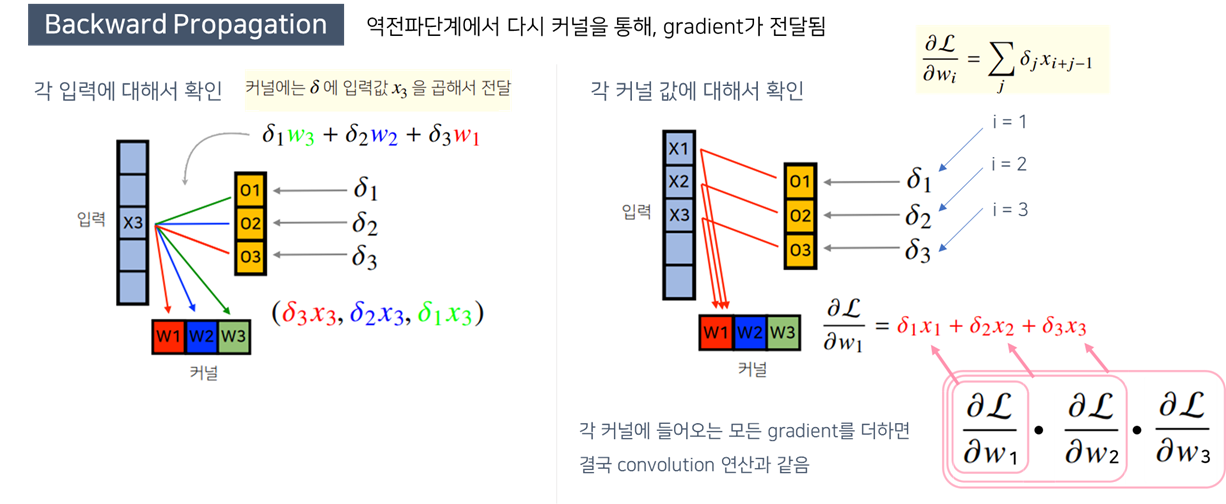
Convolution 연산의 역전파
- Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나옴
- Convolution 연산의 역전파는 선형변환
- conv 연산 수행 후에, loss function(손실함수)에서 손실값을 계산한 후, Back-propagation이 뒤에서부터 오게 됨
- 수식

- 그림설명