[DAY 12] Gradient Descent Methods
Gradient Descent의 종류
- Stochastic gradient descent
- Mini-batch gradient descent
- Batch gradient descent
Stochastic gradient descent
- 여러 데이터가 있을 때, 한번에 하나의 데이터(single sample)에 대해서만 gradient를 구하고, 그 gradient를 통해서 모델을 업데이트 ➡ 반복
Mini-batch gradient descent
- 많이 사용됨
- batch size의 샘플을 한번에 활용하여 gradient descent 구하고, 이것을 업데이트 ➡ 반복(이후 전체에서 다시 데이터 뜯어서!)
Batch gradient descent
- 한번에 모든 데이터를 다 사용
- 모든 gradient의 평균을 가지고 업데이트
- 네트워크, GPU 터지기 좋음 💥
batch size 문제
- batch size는 굉장히 중요한 파라미터 중 하나
- 큰 batch size ➡ sharp minimum에 도달
- 작은 batch size ➡ flat minimum에 도달(✔ good)
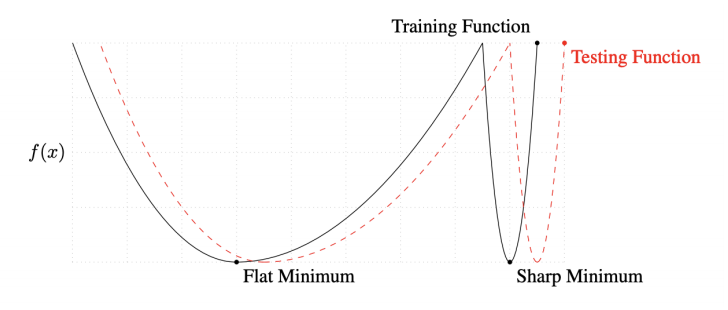
- batch size를 줄이면 일반적으로 generalization이 좋아짐을 실험적으로 보여줌
- ➡ “큰 배치사이즈를 어떻게 활용할것이냐” 중요
- Flat Minimum
- training 에서 좀 멀어져도 test에서 적당히 낮은 값이 나옴
- train에서 잘되면 test에서도 어느정도 잘되는 것을 확인
- generalization performance가 높음
- Sharp Minimun
- training 데이터를 기준으로 얻어지는 값(loss, acc) 들이 test 기준으로는 크게 다르게 나올 수 있음
- generalization performance가 낮음
Gradient Descent Methods
- Stochastic gradient descent
- Momentum
- Nesterov accelerated gradient
- Adagrad
- Adadelta
- RMSprop
- Adam
loss function 정의하고 나면, 편미분을 손으로 계산하지 않고, Automatic Differentiation(자동미분계산) 사용
tensorflow, pytorch… 등은 모두 자동미분을 지원
이제 optimizer를 골라줘야 하므로, 각각이 왜 발전했는지, 어떤 성질을 가지는지 알아야함
(Stochastic) Gradient Descent
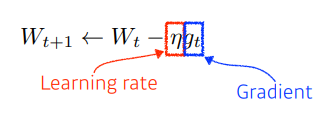
- $W$: 신경망의 weight (10만개라면, 크기가 10만인 벡터일 것)
- $g$를 자동으로 계산해줌
- 가장 기본적인 방법: lr(learning rate)만큼 곱해서 빼줌
- learning rate 적절히 잡기가 어려움
squared loss를 활용하게 되면, 큰 loss를 제곱해서 증폭시킴(MSE)
➡ 많이 틀리는 부분을 더 잘 맞추게 됨
➡ 상대적으로 덜 틀리는 부분에 대해서는 덜 집중하게 됨
➡ 그래서 아주 큰 outlier가 껴있다면 MSE를 사용하는것이 좋지 않음
Momentum
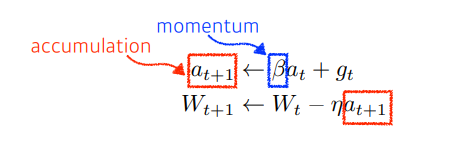
- momentum : 관성
- 같은 gradient descent를 사용하는데도 더 빠르게 학습할 수 있는 optimization 테크닉
- 어떤 쪽으로 흐르던 정보는 다음번 gradient가 조금 다르게 흐르더라도, 이전에 흐르던 방향을 어느정도 유지
- 모멘텀이 포함된 gradient로 업데이트 시키는 것
- 장점: 한번 흐르던 방향을 어느정도 유지시켜줄 수 있음(다음 회차의 gradient가 조금 다르더라도)
- ➡ gradient가 굉장히 오락가락하는 경우에도, 어느정도 잘 학습된 결과를 가져옴
minibatch training에서 모멘텀이 좋은 이유 ✔ 모멘텀: “이전의 gradient를 활용(반영)해서 다음번에도 쓰겠다” ➡ 데이터를 한번에 많이 보는 효과!
➡ 흘러온 gradient 정보가 다음에 쓰이지 않으면, 하나의 배치는 단순히 작은 영역에 영향을 미치는 데이터로서 활용됨
➡ 반면, SGD만 있다면, 많은 iteration이 있어야, 모든 데이터가 수렴할 때까지 갈 수 있음
조금더 잘 이해해보자…
Nesterov Accelerated Gradient
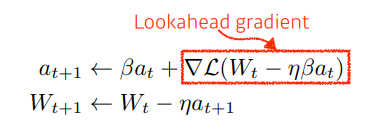
- 모멘텀과 비슷한 컨셉
- 결국, a라는 accumulate gradient가 gradient descent 역할을 함
- gradient를 계산할 때 lookahead gradient 사용
Momentum) 현재 지금 주어져있는 파라미터에서 gradient를 계산 ➡ 그 gradient를 가지고 momentum을 accumultaion
NAG) 한번 이동함 ➡ a라는 현재 정보라는게 있으면, 그 방향으로 한번 가보기 ➡ 그 곳에서의 gradient를 계산한 것을 가지고 accumulate하기
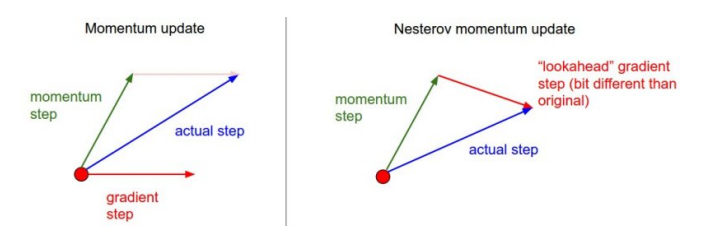
- 모멘텀의 문제: 관성이라고 생각하면, local minimum에 converging(수렴)을 못함 ➡ 계속 지나침
- NAG: 한번 지나간 곳에서의 gradient를 계산하니까 local minima가 한쪽 아래로 흘러가는 효과
- 봉우리에 훨씬 빠르게 수렴(Convergence)
모르겠다
여기까지는 관성을 이용한 방법
Adagrad
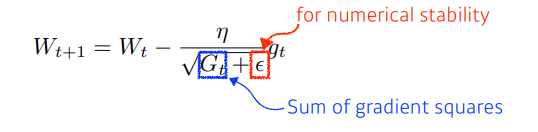
- NN 파라미터가 많이 바뀌었는지, 적게 바뀌었는지 확인
- 적게 변한건 더 크게 변하게 하고, 크게 변한건 더 작게 변하게 함
- 문제: $G_t$가 계속 커짐
- $G$가 계속 커지면 분모가 무한대니까 $W 업데이트가 안이뤄질 것
- ➡ 뒤로 갈수록 학습이 점점 안되는 문제점이 발생
이를 해결하기 위해 다른(뒤)방법이 있음- Sum of gradient squares: 얼만큼 변했는지를 제곱해서 더한것 ➡ 계속 커질 것
- ➡ 커진다는건, 지금까지 많이 변했다는 의미이고, 이를 역수에 넣으니까
- ➡ 많이 변한건 적게변하고, 적게변한건 많이 변하게 됨
Adadelta

- Adagrad가 가지는 문제를 해결하고자 쓰임 ➡ $G_t$가 계속 커지는 현상을 막고자 함
- Adadelta는 Adagrad에서 가지고 있던, $lr$이 $G_t$로 표현됨으로써 생기는 Monotonically Decreasing Property를 막는 방법
- 가장 쉬운 방법
- 현재 타임스텝 t가 주어졌을 때, 어느 정도의 window사이즈 만큼의 파라미터, 시간에 대한 gradient 제곱의 변화를 보기
- 문제: 윈도우 사이즈가 100이면, 이 100이라는 윈도우 사이즈만큼은 계속 정보를 들고있어야한다는 것
- ➡ 파라미터 양이 아주 많으니까 그냥 이렇게 하면 GPU 터지기 좋음!
- 해결: Exponential Moving Average
- EMA
- 어떤 값이 있을 떄, 감마와 이전값에 감마와 곱하고, 옴 마이너스 감마 만큼을 더해주면 어느정도 time window 만큼의 값을 저장하고있는, 그것에 대한 합으로 볼 수 있게 됨
- EMA of difference squares: 실제 변화시키려는 weight의 변화값 ➡ 그래서 lr이 없어도 어느정도 가능하게 만들겠다는 것
adadelta는 learning rate가 없음
바꿀 수 있는 요소가 많이 없기 떄문에 잘 활용되지 않음
모르겠음
RMSprop
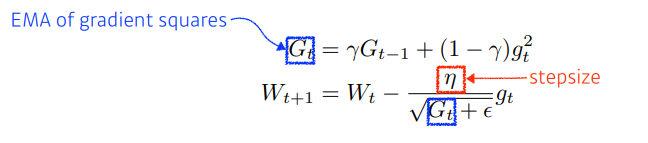
- $G_t$를 그냥 더하지 않고, Exponential Moving Average 더해줌
- 그것을 분모텀에 넣고 step size를 넣음
많이 사용
논문을 통해서 제안된 것이 아닌, practical 제안
모르겠음
Adam

- 모멘텀과 adaptive learning rate를 합친 것 ➡ 일반적으로 성능이 좋음
- 특징
- gradient의 크기가 변함에 따라서 (혹은 gradient의 square의 크기에 따라서) adaptive하게 learning rate를 바꿈
- 이전의 gradient 정보에 해당하는 모멘텀 두개를 합친 것
4개의 중요 파라미터 (어떻게 조정할 지가 중요)
- $\beta_1$: 모멘텀을 얼마나 유지시킬 것인가
- $\beta_2$: Gradient Squares에 대한 EMA 정보
- $\eta$ (=lr, learning rate)
- $\epsilon$ (=입실론)
adaptive learning rate
어느 파라미터에서는 lr을 줄이고 어떤 파라미터의 lr은 높일 수 있음
따라서, 같은 base learning rate를 가지고 있다 하더라도 훨씬 더 빠르게 학습 가능
