[DAY 14] RNN
- 시계열 데이터, sequential 데이터에 주로 사용됨
- 데이터가 독립적이지 않을 때
시퀀스 데이터
시퀀스 데이터란?
- 순차적으로 들어오는 데이터
- 이벤트의 발생 순서가 중요한 경우
- ex) 소리, 문자열(문맥, 의도, 문법), 주가(시장의 상황, 사건의 발생이 시점별로 나타남)
- 독립동등분포(i.i.d.) 가정을 잘 위배하기 때문에 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀌게 됨
- 앞뒤 맥락이 중요
- 데이터의 순서를 함부로 바꿔서 인위적으로 조작하면 학습이 잘 되지 않음
시퀀스 데이터 다루는 방법
- 순차적으로 들어오는 정보를 어떻게 다룰까?
- 이전 시퀀스의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다루기 위해 조건부확률을 이용
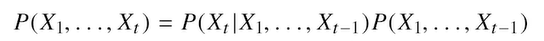

베이즈법칙 사용
조건부확률은 곱셈을 사용
이전까지의 확률을 전부 곱한 것을 사용
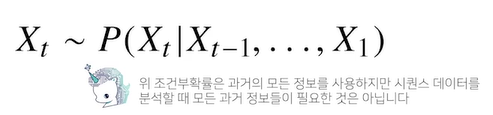
- 가장 최근의 정보를 주로 다루는 경우가 많기 때문에, 과거의 데이터의 영향력은 최근의 영향력보다 적어야하는 경우가 있음
- 필요성에 따라 과거의 데이터를 어떻게 활용할지 정해야함
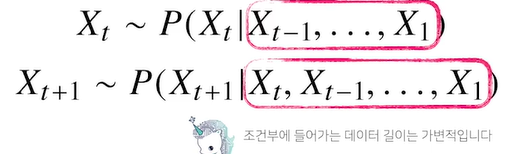
- 각각의 시점에서 다뤄야하는 데이터의 길이가 다르기 때문에 - ?!
- 시퀀스 데이터를 다루기 위해서는 길이가 가변적인 데이터를 다룰 수 있는 모델이 필요 (➡ 잠재변수를 사용함으로서 해결(자기회귀적))

- 위와 같이 고정된 크기를 가지고 예측시, auto regressive model중에서도 period가 $\tau$인 경우에 해당하므로, 이런 형태의 모델링으로도 시퀀스 데이터를 다룰 수 있음
- 문제: $\tau$는 hyper parameter(모델링 하기 전에 사전에 정의해줘야하는 변수)
- $\tau$를 정해주는 것만으로도 사전지식이 필요한 경우가 있음
- 문제에 따라 $\tau$가 달라질 수 있음
- $\tau$가 작을수도있고(과거 정보를 많이 포함하지 않음), 클수도 있음(과거 정보를 많이 포함)
- 이때 사용되는 것이 RNN이 Latent Auto Regression Model(잠재 자기회귀모델)
- 직전정보와 직전정보가 아닌 훨씬 이전인 과거의 정보를 따로 모아서 처리

- $H_t$: 잠재변수
- $X_t$를 구할 때, $X_{t-1}$과 잠재변수 $H_t = X_{t-2}, … , X_1$ 사용
- 직전의 정보와 잠재정보를 가지고 미래 예측가능. 이제부터는 가변적이지않은, 고정적인 모델을 모델링할 수 있음
- 장점
- 과거의 정보를 따로 처리해줄 수 있음 - 과거의 모든 데이터를 가지고 예측에 사용할 수 있음
- 가변적데이터 문제를 고정적 데이터 문제로 바꿀 수 있음
- 문제) 과거의 정보를 어떻게 인코딩 할 것인가? -> RNN
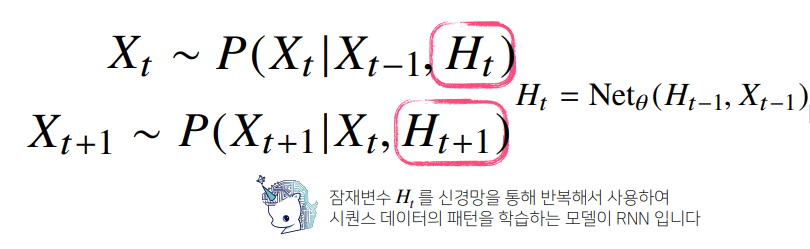
- NN을 통해 과거(바로 이전) 정보와 과거의 잠재변수들을 가지고 모델링을 할수 있는 예측할 수 있는 모델: RNN(seq data 학습)
RNN
Forward Propagation
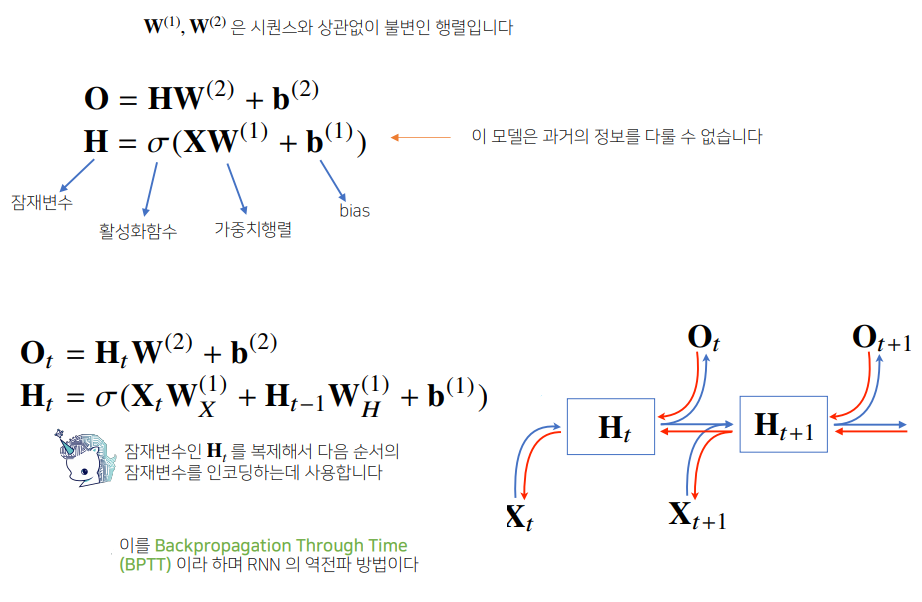
- 가장 기본적인 RNN 모형은 MLP와 유사
- W1, W2는 시퀀스에 상관없이 동일하게 적용
- 위의 식은 과거의 정보를 다룰 수 없음! 왜냐면 입력이 t번째 데이터(현재)만 들어오게 되므로
- 아래의 식에 새로운 식이 추가됨
- $W_H$
- $X_t$: 현재들어온 입력벡터
- $H_{t-1}$: 이전시점의 잠재변수
- $H_t = X_t + H_{t-1}$: 현재 시점의 잠재변수
- 이 $H_t$를 사용해서 현재 시점의 output $O_t$를 만들어냄
- $H_t$는 다음 시점의 $H_{t+1}$을 인코딩하는 데에 사용 됨
- 가중치 행렬이 3개 나오게 됨 ➡ t에 따라 변하는 것이 아님
- $W_X^{(1)}$: 첫번째 레이어에서 입력데이터에서부터 선형모델을 통해서 잠재변수로 인코딩
- $W_H^{(1)}$: 이전시점의 잠재변수를 받아서 현재 시점의 잠재변수로 인코딩
- $W^{(2)}$: 출력으로 만들어줌, 출력을 뱉음
t에 따라 변하는 것: 입력데이터와 잠재변수
가중치 행렬, $W_X^{(1)}$, $W_H^{(1)}$, $W^{(2)}$: t에 따라 변하지 않음, 각각 t 시점에 모델링에 활용되는 것 뿐
Backward Propagation
- 계산(computational)그래프의 거꾸로 흐름
- RNN에서의 모든 예측이 이루어진 다음, 맨 마지막 시점에서의 gradient가 점점 타고타고 올라와서 과거까지 gradient가 흐르는 것 ➡ BPTT라는 역전파 방법
- 잠재변수에 들어오는 gradient: 2개
- 바로 다음시점에서의 잠재변수에서 들어오는 gradient vector
- 출력에서 오는gradient vector
- ➡ 그리고 이것을 입력과 이전시점의 잠재변수에 전달
BPTT

- 역전파 방법
- RNN의 가중치 행렬의 미분을 계산하면 아래와 같이 미분의 곱으로 이루어진 항이 계산됨
- 모든 t 시점에서의 손실함수를 계산한 후, 전달할 gradient를 계산
- BPTT를 통해서 각 가중치 행렬을 미분했을 때, 최종적으로 나오는 product term(i+1 ~ t 시점까지의 모든 잠재변수에 대한 미분텀이 곱해져서 더해짐), 현재부터 더해야하는 길이 T가 길어질수록 곱해지는 term들이 불안정해지기 쉬움
- (이 항이 1보다 크면)미분값이 너무 커지거나 (이 항이 1보다 작으면)너무 작아질 수 있는 가능성이 있음
- 그래서 BPTT를 일반적인 모든 상황에 적용하게 되면 네트워크의 학습이 불안정해 짐(gradient를 전부 곱해주는 형태이기 때문)
BPTT의 기울기 소실 문제
- gradient를 계속 곱하는 문제
- gradient vanishing 문제(기울기가 0으로 계속 사라짐)
- 과거정보를 무시하게 됨(과거정보를 잃어버리면, 조금 긴, 문맥이 중요한 문장의 해석 같은 경우가 힘들수있음)
- 시퀀스 길이가 길어지는 경우 BPTT를 통한 역전파 알고리즘의 계산이 불안정해지므로, 길이를 끊는 것이 필요 ➡ Truncated BPTT
- 잠재변수에 들어오는 gradient를 볼 때, (미래시점~t+1시점)의 gradient는 받고, 여기서 받은 gradient는 H_t에 전달하지 않고, 특정 블럭에서 끊는 방식
- 이 방법을 통해서 기울기 소실 해결!
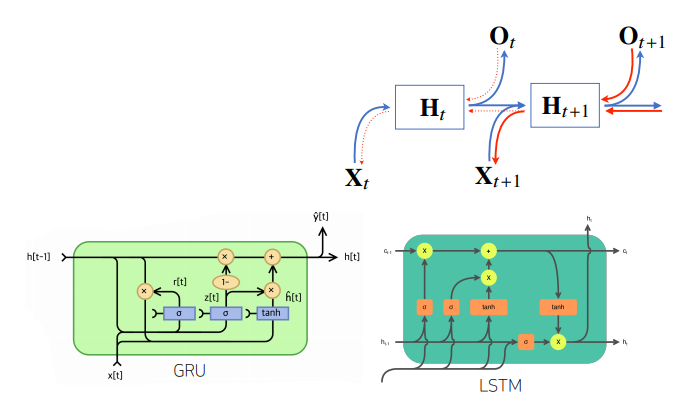
(그러나 이 방법들 대신에, 길이가 긴 시퀀스 데이터 처리를 위해서는 조금 더 발전된 RNN 모델인 LSTM, GRU 사용)
- 앞선 문제들 때문에 Vanilla RNN은 길이가 긴 시퀀스를 처리하는 데 문제가 있음
- 이를 해결하기 위해서 등장한 RNN 네트워크가 LSTM과 GRU 사용!

