[DAY 21] 그래프 기초
그래프의 구성
- 그래프: 정점 집합과 간선 집합으로 이루어진 수학적 구조 (=네트워크)
- 정점: vertex, node
- 간선: edge, link
필수 기초 지식
- 하나의 간선은 두 개의 정점을 연결한다.
- 모든 정점 쌍이 반드시 간선으로 직접 연결되는 것은 아니다.
- 그래프(Graph)는 정점 집합과 간선 집합으로 이루어진 수학적 구조이다.
- 보통 정점들의 집합을 𝑽, 간선들의 집합을 𝑬, 그래프를 𝑮 = (𝑽, 𝑬)로 적는다.
그래프의 이웃
- 정점의 이웃(Neighbor)은 그 정점과 연결된 다른 정점을 의미한다.
- 정점 𝑣의 이웃들의 집합을 보통 𝑵(𝒗) 혹은 𝑵𝒗로 적는다.
- 나가는 이웃, 들어오는 이웃
- 방향성이 있는 그래프에서는 나가는 이웃과 들어오는 이웃을 구분한다.
- 정점 𝑣로 간선이 들어오는 이웃(In-Neighbor)의 집합을 보통 𝑵in(𝒗)로 적는다.
- 정점 𝑣에서 간선이 나가는 이웃(Out-Neighbor)의 집합을 보통 𝑵out(𝒗)로 적는다.
- 그래프를 다루기 위해 파이썬 라이브러리인 NetworkX를 사용하면 편리하다. - 실습 1-1 참고
그래프가 중요한 이유
- 우리 사회는 많은 복잡계(Complex System)으로 이루어져 있다.
- 그래프와 복잡계는 둘 다, 구성요소 간의 복잡한 상호작용이다.
- 따라서 복잡계를 그래프로 표현할 수 있다.
그래프는 복잡계를 표현하고 분석하기 위한 언어
- 복잡계는 구성 요소들 간의 상호작용으로 이루어진다.
- 상호작용을 표현하기 위한 수단으로 그래프가 널리 사용된다.
- 복잡계를 이해하고, 복잡계에 대한 정확한 예측을 하기 위해서는 복잡계 이면에 있는 그래프에 대한 이해가 반드시 필요!
그래프 관련 인공지능 문제
- 정점 분류(Node Classification) 문제
- 각 정점의 유형을 추측할 수 있다.
- 같은 유형의 노드는 같은 색을 띈다.
- 어떤 유형인지 모르는 노드가 주어졌을 때, 이어지는 노드의 유형을 통해, 새로 들어온 노드의 유형을 추측할 수 있다.
- 예시
- 트위터에서의 공유(Retweet) 관계를 분석하여, 각 사용자의 정치적 성향을 알 수 있을까?
- 단백질의 상호작용을 분석하여 단백질의 역할을 알아낼 수 있을까?
- 연결 예측(Link Prediction) 문제
- 거시적 관점: 주어진 그래프가 어떻게 성장할 지 예측한다.
- 미시적 관점: 각 정점이 앞으로 어떤 정점과 연결될 지 예측한다.
- 예시: 페이스북 소셜네트워크는 어떻게 진화할까?
- 추천(Recommendation) 문제
- 기존에 주어진 구매 정보를 기반으로 예측하여 추천해준다.
- 예시: 각자에게 필요한 물건은 무엇일까? 어떤 물건을 구매해야 만족도가 높을까?
- 군집 분석(Community Detection) 문제
- 군집: 서로 밀접하게 연결된 집합
- 군집 내의 관계는 의미있는 구조를 나타내는 경우가 많다. (기계학습 클러스터링과 유사)
- 연결 관계로부터 의미있는, 사회적 무리(Social Circle)을 찾아낼 수 있을까?
- 랭킹(Ranking) 및 정보 검색(Information Retrieval) 문제
- 웹(Web)이라는 거대한 그래프로부터 어떻게 중요한 웹페이지를 찾아낼 수 있을까?
- 정보 전파(Information Cascading) 및 바이럴 마케팅(Viral Marketing) 문제
- 정보는 네트워크를 통해 어떻게 전달될까? 어떻게 정보 전달을 최대화 할 수 있을까?
- 그래프 신경망(Graph Neural Networks)
그래프의 유형 및 분류
- 방향성
- 간선에 방향이 없는 그래프(Undirected Graph): 대등한 관계를 표현 - 협업 관계 그래프, 페이스북 친구 그래프
- 간선에 방향이 있는 그래프(Directed Graph): 주체와 대상을 분리 - 인용 그래프, 트위터 팔로우 그래프
- 가중치
- 간선에 가중치가 없는 그래프(Unweighted Graph): 웹 그래프, 페이스북 친구 그래프
- 간선에 가중치가 있는 그래프(Weighted Graph): 전화 그래프, 유사도 그래프
- 노드의 종류
- 동종 그래프(Unpartite Graph): 단일 종류의 정점을 가짐, 단일 종류의 정점을 가집니다 - 웹 그래프, 페이스북 친구 그래프
- 이종 그래프(Bipartite Graph): 두 종류의 정점을 가짐, 다른 종류의 정점사이에만 간선이 연결 - 전자 상거래 구매내역(사용자, 상품), 영화 출연 그래프 (배우, 영화)
그래프의 구현 및 저장
간선 리스트 (Edge List)
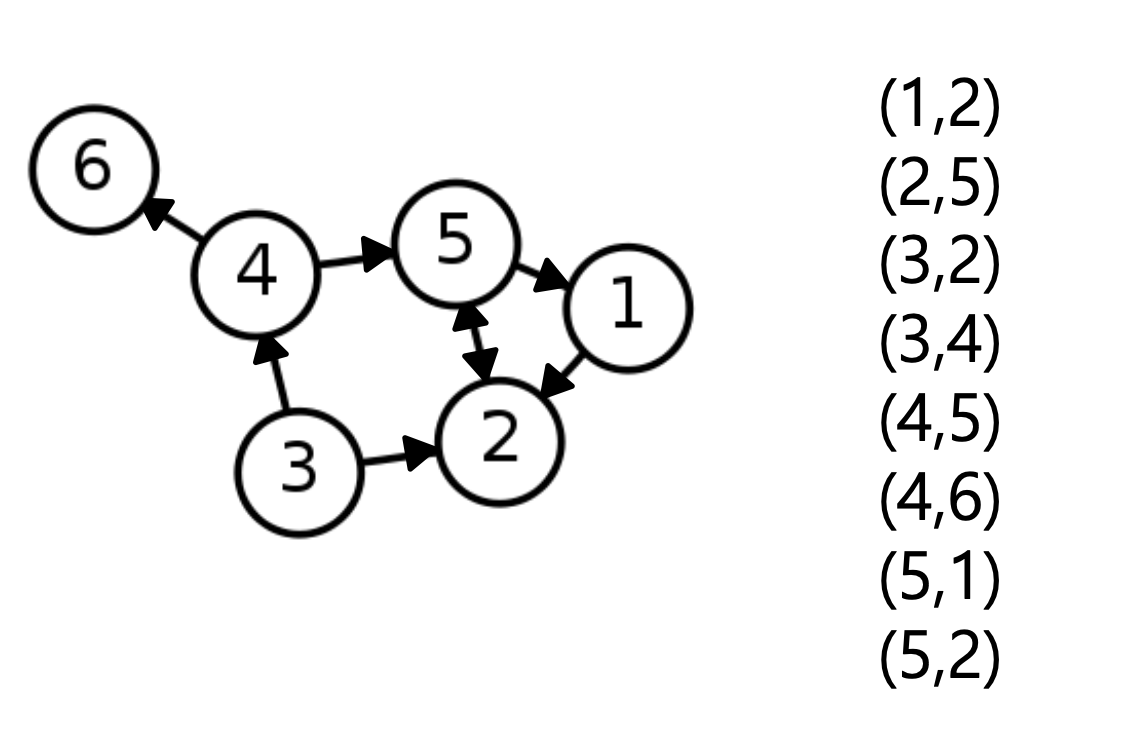
- 그래프를 간선들의 리스트로 저장
- 각 간선은 해당 간선이 연결하는 두 정점들의 순서쌍(Pair)으로 저장
- 방향성이 있는 경우에는 (출발점, 도착점) 순서로 저장
- 그래프 내에 없는 간선을 찾기 위해서는 리스트를 끝까지 찾아봐야 한다는 단점이 있다.
인접 리스트 (Adjacent list)
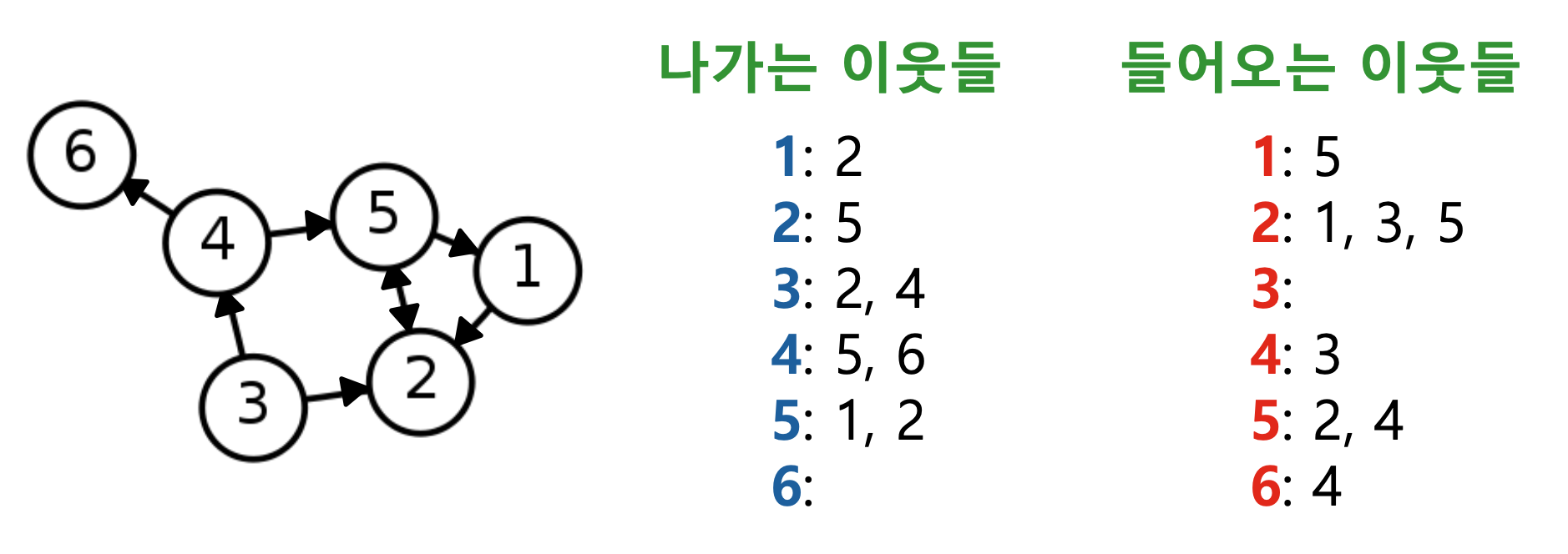
- 방향성이 없는 경우에, 하나의 edge는 연결된 각 vertex에 의해 두 번 등장한다.
- 방향성이 있는 경우, 나가는 이웃들과 들어오는 이웃들을 각각 리스트로 저장할 수 있다.
인접 행렬(Adjacency Matrix)
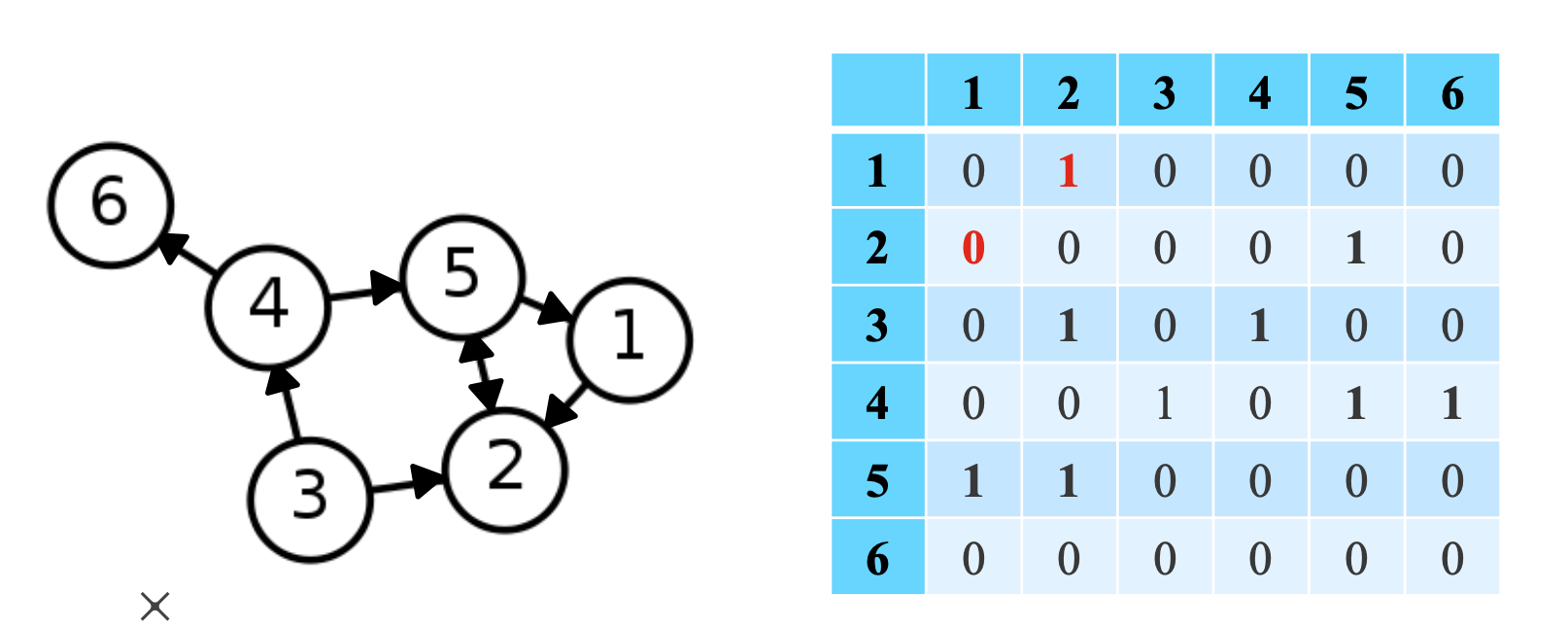
- 정점 수 × 정점 수 크기의 행렬
- 방향성이 없는 경우
- 정점 𝑖와 𝑗 사이에 간선이 있는 경우, 행렬의 𝑖행 𝑗열 (그리고 𝑗행 𝑖열) 원소가 1
- 정점 𝑖와 𝑗 사이에 간선이 없는 경우, 행렬의 𝑖행 𝑗열 (그리고 𝑗행 𝑖열) 원소가 0
- 방향성이 있는 경우
- 정점 𝑖에서 𝑗로의 간선이 있는 경우, 행렬의 𝑖행 𝑗열 원소가 1
