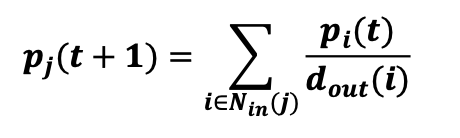[DAY 22] Page Rank
검색엔진에서는 그래프를 어떻게 활용할까?
웹과 그래프
- 웹은 웹페이지와 하이퍼링크로 구성된 거대한 방향성 있는 그래프라고 볼 수 있다.
- 웹페이지는 정점에 해당한다.
- 웹페이지가 포함하는 하이퍼링크는 해당 웹페이지에서 나가는 간선에 해당한다.
- 단, 웹페이지는 추가적으로 키워드 정보를 포함하고 있다.
페이지랭크가 나오게 된 계기?
검색엔진의 기존 방식
- 웹을 디렉토리로 정리
- 카테고리의 수와 깊이가 너무 커짐
- 카테고리 구분이 모호한 경우가 많음
- 키워드에 의존한 검색엔진
- 사용자가 입력한 키워드에 대해, 해당 키워드를 (여러 번) 포함한 웹페이지를 반환
- 악의적인 웹페이지에 취약하다는 단점
- 성인사이트가 ‘축구’라는 키워드를 보이지않게 많이 포함시키면, 축구의 연관 페이지가 된다.
- 페이지랭크
- 사용자 키워드와 관련성이 높고 신뢰할 수 있는 웹페이지를 찾기위한 방법으로 고안되었다.
페이지랭크의 정의
페이지랭크는 두가지 관점에서 정의될 수 있다.
- 투표 관점
- 임의보행 관점
1. 투표 관점
- 투표를 통해 사용자 키워드와 관련성이 높고 신뢰할 수 있는 웹페이지를 찾는다.
- 투표 주체: 웹페이지
- 투표 방법: 하이퍼링크를 통해 투표
- 어떤 웹페이지가 하이퍼링크를 포함할 때, 하이퍼링크에 걸린 웹페이지를 신뢰한다는 것을 의미
- 하이퍼링크에 연결된 웹페이지에 한 표를 투표한다고 생각!
🔍 웹페이지 𝑢가 𝑣로의 하이퍼링크를 포함한다면?
𝑢의 작성자가 판단하기에 𝑣가 관련성이 높고 신뢰할 수 있다는 것을 의미한다.
즉, 𝑢가 𝑣에게 투표했다고 할 수 생각할 수 있다.
해석: 들어오는 간선이 많을수록 신뢰할 수 있다는 뜻! → 논문을 고를 때도 마찬가지로, 사람들은 많이 인용된 논문을 더 많이 신뢰한다.
- 문제점
- 들어오는 간선의 수를 세는 것은 악용될 소지가 있다.
- 조작된 웹페이지를 여러 개 만들어서 간선의 수를 부풀릴 수 있다.
돈을 주고 들어오는 간선의 수를 늘리는 것이다. 즉, 관련성과 신뢰도가 높아 보이도록 조작할 수 있다.
- 해결책
- 이런 악용에 의한 효과를 줄이기 위해, 페이지랭크에서는 가중 투표를 한다.
- 즉, 관련성이 높고 신뢰할 수 있는 웹사이트의 투표를 더 중요하게 간주한다. 반면, 그렇지 않은 웹사이트들의 투표는 덜 중요하게 간주한다. 악용이 없는 경우에도 사용할 수 있는 합리적인 투표 방법이다.
- → 좀 더 믿을만한 웹페이지의 가중치를 더 높게 측정하는 것이다.
- 결국, 출력을 입력으로 사용하게 되는 재귀, 연립방정식 풀이를 통해서 사용할 수 있다. (입력과 출력 모두 관련성과 신뢰성에 대한 측정량이므로!)
투표 관점에서의 간단한 식 정리
- 측정하려는 웹페이지의 관련성 및 신뢰도를 페이지랭크 점수라고 부르자.
- 각 웹페이지는 각각의 나가는 이웃에게 자신의 페이지랭크 점수 만큼의 가중치로 투표를 한다.
- (자신의 페이지랭크 점수)/(나가는 이웃의 수) 만큼의 가중치로 투표한다.

- 각 웹페이지의 페이지랭크 점수는 (이웃들에 의해) 받은 투표의 가중치 합으로 정의된다.


2. 임의 보행 관점
- 페이지랭크는 임의 보행(Random Walk)의 관점에서도 정의할 수 있다.
- 임의 보행을 통해 웹을 서핑하는 웹서퍼를 가정하자.
- 즉, 웹서퍼는 현재 웹페이지에 있는 하이퍼링크 중 하나를 균일한 확률로 클릭하는 방식으로 웹을 서핑한다.
- 웹서퍼가 𝑡번째 방문한 웹페이지가 웹페이지 𝑖일 확률을 𝒑𝒊(𝒕) 라고 하자.
그러면 𝒑(𝒕)는 길이가 웹페이지 수와 같은 확률분포 벡터가 된다. 그러면 아래 식이 성립한다.

- p(t)는 벡터가 되고, v개의 p 값이 존재한다.
- $p_i(t)$는 $i$→$j$ 확률을 $j$에 들어오는 각각에 계산
- $p_j(t+1)$는 $t+1$번 째 방문한 웹페이지가 $j$일 확률

- $p(t) = p(t+1) = p$가 수렴한다는 것은 $t$가 충분히 커서, 각각 $p_i, p_j$가 된다는 것
페이지 랭크 점수

페이지랭크의 계산: 반복곱

- $r_i^{(0)}$: 0번째 iteration 점수
- $r^{(t)} \approx r^{(t+1)}$인 경우, 종료 (충분히 유사해진 경우)
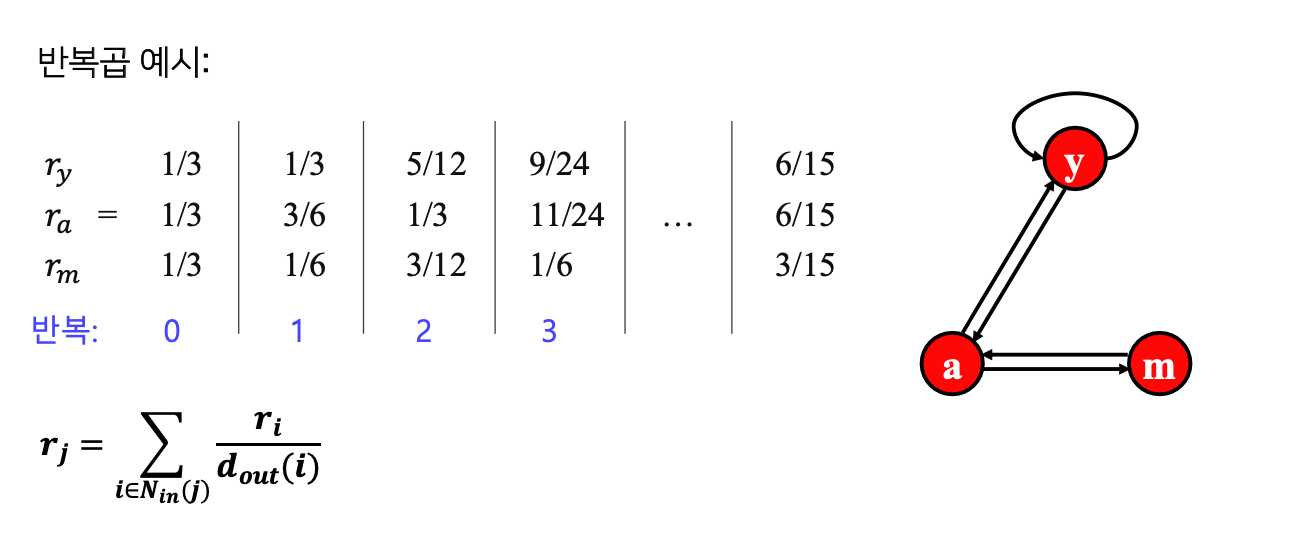
마지막 iteration에서 $6/15, 6/15, 3/15$로 수렴성을 만족한다. → $p(t) \approx p(t+1)$
- 문제점
- 반복곱이 항상 수렴하는 것을 보장할 수 없다.
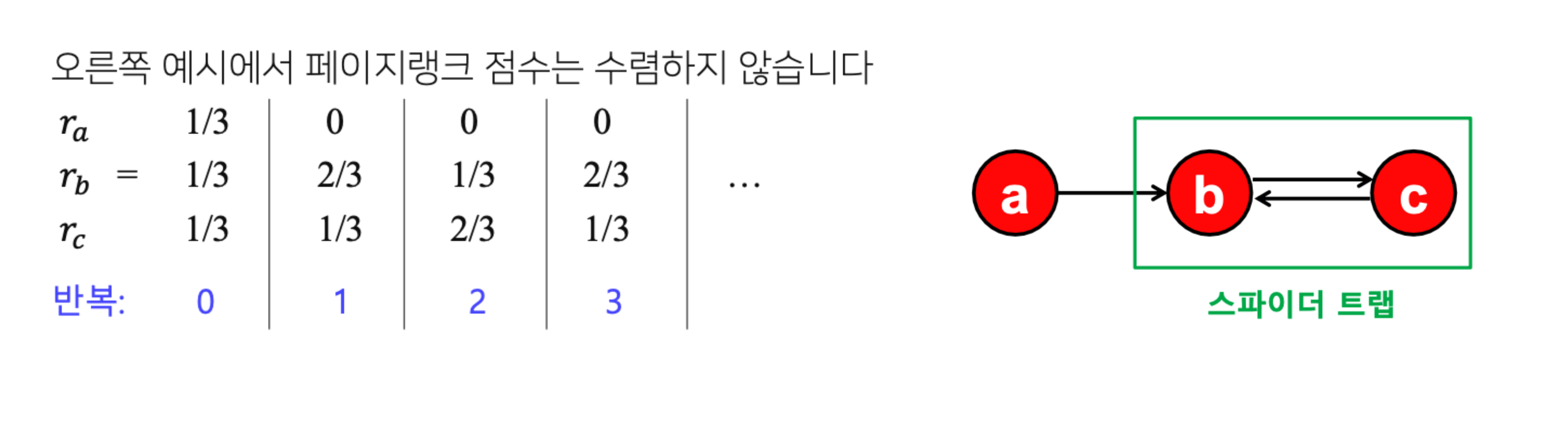
- 들어오는 간선은 있지만 나가는 간선은 없는 정점 집합인 스파이더 트랩(Spider Trap) 에 의한 문제
- 수렴하지 않는다.

- 반복곱이 합리적인 점수로 수렴하는 것을 보장할 수 없다.
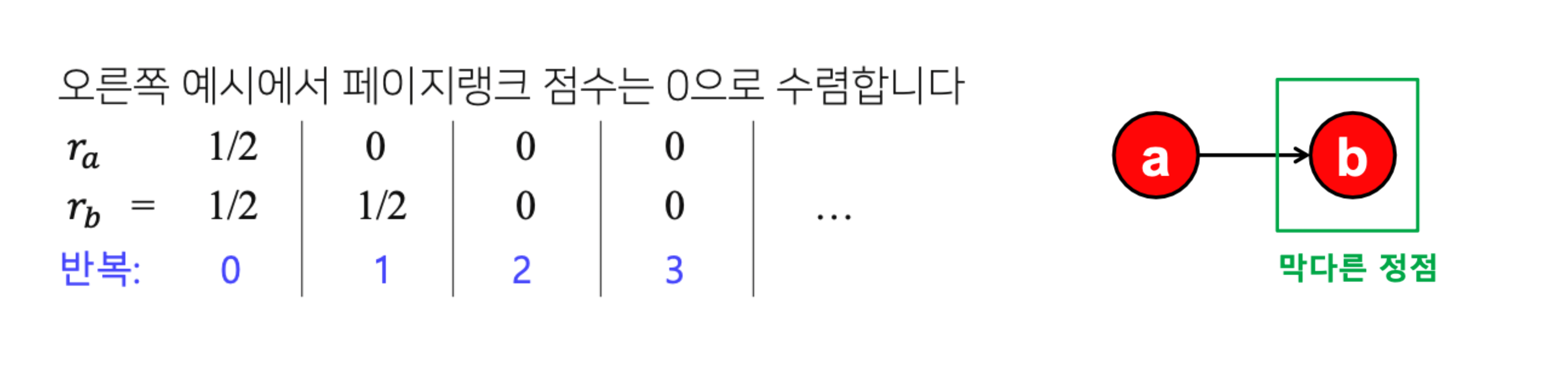
- 들어오는 간선은 있지만 나가는 간선은 없는 막다른 정점(Dead End) 에 의한 문제
- 페이지랭크 점수가 0에 수렴할 수 있음

- 반복곱이 항상 수렴하는 것을 보장할 수 없다.
- 해결책
- 순간이동(Teleport)

- (1)과 (4)의 임의의 웹페이지는 전체 웹페이지들 중에 하나를 균일확률로 선택
- 순간이동에 의해서 스파이더 트랩이나 막다른 정점에 갇히는 일이 없어진다.
- 𝛼를 감폭 비율(Damping Factor) 이라고 부르며 값으로 보통 0.8 정도를 사용
순간이동을 도입하면 페이지랭크 점수 계산이 아래와 같이 바뀐다. (임의보행 확률적 해석에 의해 해석)

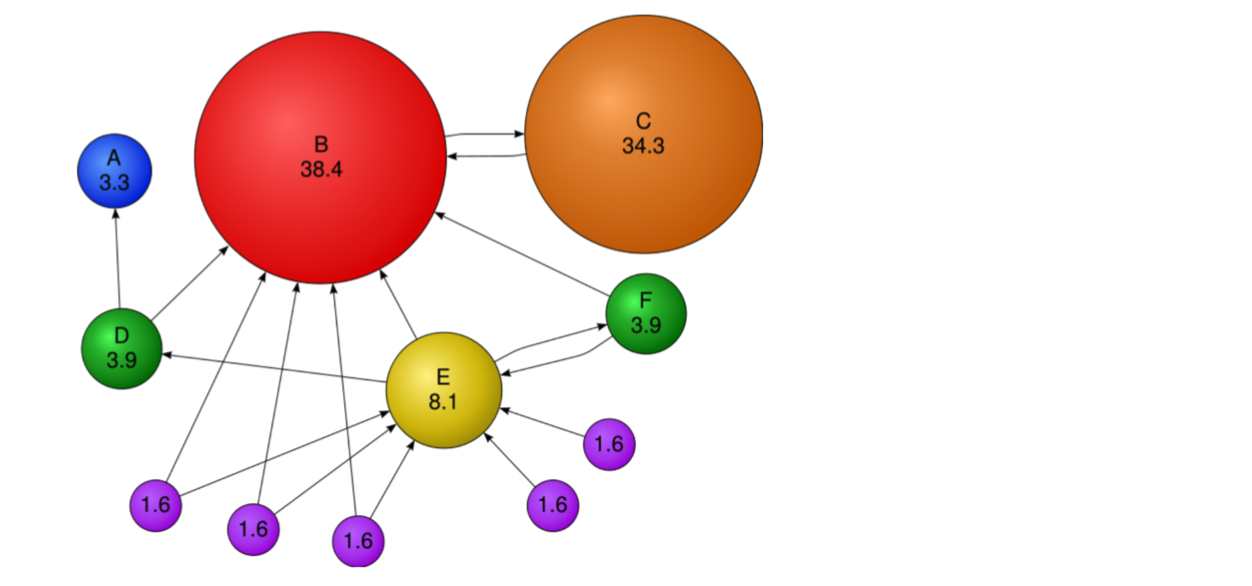
- 결과 (수정된 페이지랭크 점수 예시)

- 가장 투표를 많이받은 정점은 신뢰할 수 있는 정점이 되므로, 신뢰할 수 있는 정점이 가리키는 C라는 정점에 대한 신뢰도도 높아지는 것을 볼 수 있다.