[DAY 22] Page Rank의 수도코드와 해석
Page Rank의 수도코드

기초지식 (Review)
- 페이지랭크 값은 투표를 통해서 결정된다.
- 들어오는 값이 많을수록 해당 노드(웹페이지)의 신뢰도가 높다고 판단한다.
- 들어오는 값은 모두 같은 값이 아니다.
자신의 페이지랭크 점수 정하는 방법
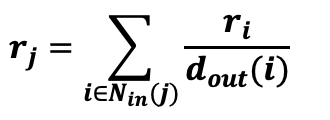
$r_j$: $j$ 웹페이지의 페이지랭크 점수
$N_{in}(j)$: $j$ 웹페이지(정점)에 들어오는 간선
$d_{out}(i)$: $i$ 웹페이지($j$로 들어가는 정점)의 나가는 간선의 수
결국, 이 값이 의미하는 바는, 투표 관점에서 봤을 때…
- 점수 계산하는 방법: 자신으로 들어오는 모든 노드에 대해, (해당 노드의 페이지랭크 값)/(해당 노드의 나가는 간선 수) 이다.
- 따라서 자신으로 들어오는 노드의 페이지랭크 값이 클수록, 그 노드의 나가는 간선 수가 적을수록 “나”에게 매겨지는 값이 커진다는 것이다.
- 그리고 이것을 몇 번의 iteration을 통해(반복곱) 여러번 페이지랭크를 계산하다보면, 결국 수렴하는 (각각의) 페이지 랭크 점수를 가지게 될 것이다. (이 부분은 KNN과 비슷하다고 생각함)
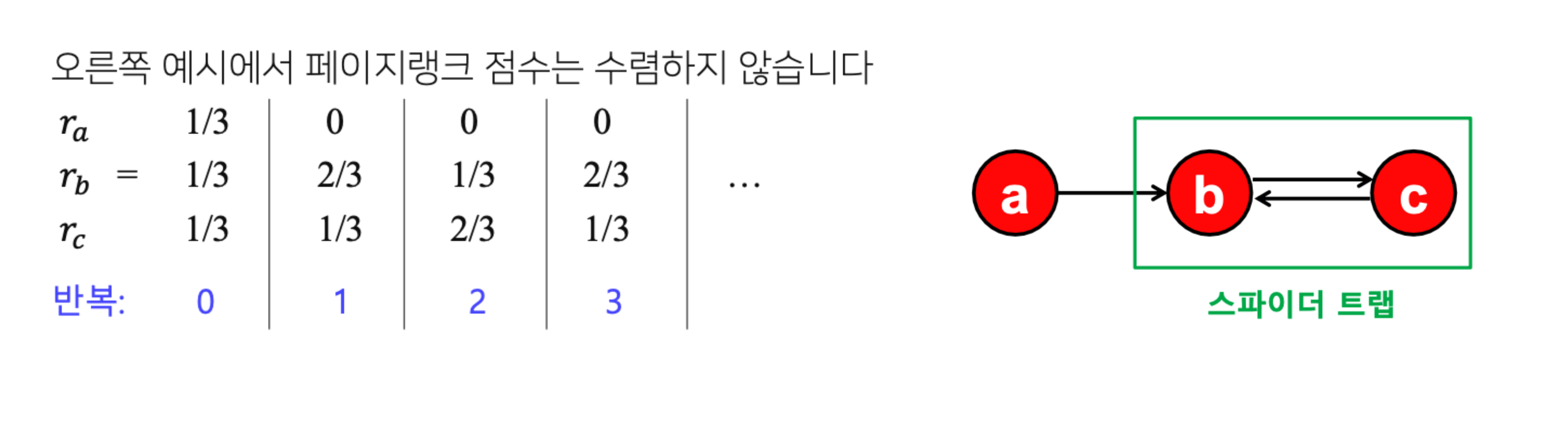
문제점 1: 스파이더 트랩 (Spider Trap)
- 원인: 서로를 가리킴

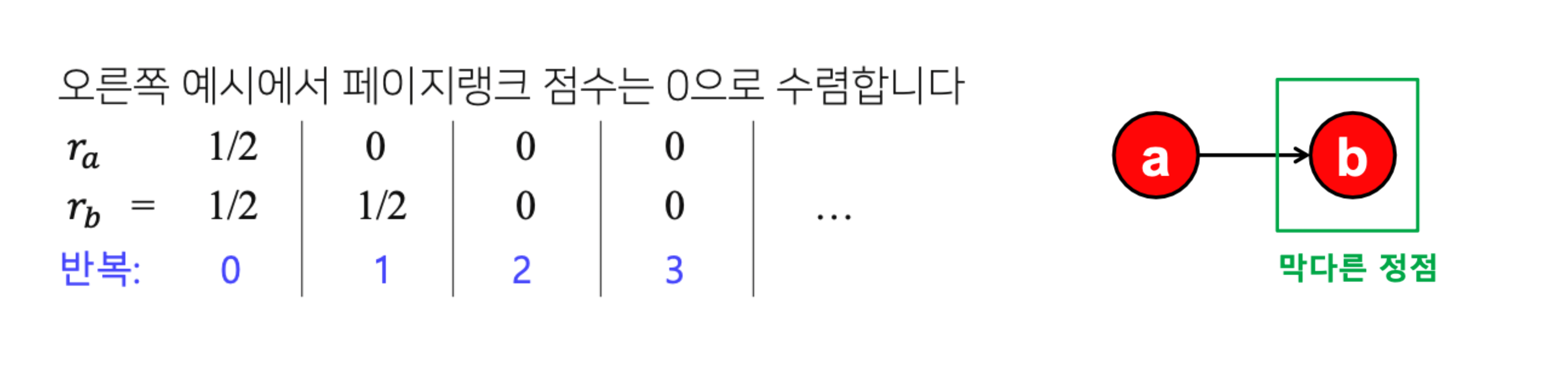
문제점 2: 막다른 정점 (Dead End)
- 원인: 들어오는 간선은 있는데, 나가는 간선이 없음

🔍 여기서 이해가 안갔던 점은, $r_a$에서 먼저 0값이 되어버렸다는 것이다. Dead End의 정의를 보면, 나가는 간선이 없어서 생긴다고 했는데, 왜 들어오는 간선이 없는 쪽인 a의 값이 먼저 0이 되어버린 것일까?
아마도, “나가는 간선이 없어서, 들어오는 것도 없다.”라고 생각할 수 있을 것이다. 들어오는 곳이 있으면, 나가는 곳도 있듯이, 나가는 곳이 있어야 들어오는 곳이 생긴다. 근데, 나가는 곳이 없다. 그래서 들어오는 곳이 없어진 $r_a$가 먼저 0이 되어버린 것이 아닐까? - ??
해결책: 순간이동
- 어떠한 확률로, 순간이동 투표를 한다.(무작위 투표를 한다.)
- 그러면 막다른 정점에서 어디론가 나가는 간선이 생김을 의미하고(데드엔드 해결), 스파이더 트랩으로 인해 수렴하지 못하던 값이 순간이동?해서 외부로 나갈 수 있게 된다!(스파이더 트랩 해결)
- 순간이동 할 확률: $\alpha$ = 감폭비율(Damping Factor)
순간이동은 뭐랄까, 개인적으로 해석하자면, 사용자가 가끔 하던 방식으로 웹페이지를 서칭하지 않고, 다른 웹사이트에도 방문할 수 있는 확률을 넣어준 것이 아닐까…
최종적으로 우리가 사용할 수식은 아래와 같다.

어쨌든, 이제 수도코드와 비교해서 보자.

근데 코드와 식을 비교해서 보면 이상한 값이 나온다. 바로 $S$이다. 왜 $\beta$와 $S$를 따로 써주는 것일까?
그 이유는 다음과 같다.
page rank 점수 총 합을 1로 맞춰주기 위함이다.
시작 부분을 보면, $|V|$개의 정점을 $1 \over |V|$ 값으로 초기화해준다. 결국 총 합은 1이다.
총합은 처음에도 1이고, iteration을 돌면서도 계속 1을 만족해야한다. 그래야 dead end 없이 (유실되는 값 없이) 총량이 유지된다고 볼 수 있기 때문이다.
만약 Dead End를 유발하는 정점이 있다고 생각해보자.(나가는 간선이 없음) 그러면, $S$는 1보다 작아질 것이다. 왜냐면 $r_j^{new}$ 를 구하는 9번 라인에서 볼 수 있듯이, out된 간선의 가중치를 받아서 다른 노드들의 페이지랭크 점수를 계산해야하는데, 어떤 노드가 out을 주지 않으니, 다른 노드들은 자신이 받아야하는 가중치 총량 중 일부를 못받게 되는 것이다!
이를 막기 위해서, 일반적인 페이지랭크 계산을 먼저 진행하고, 1에서 계산된 페이지랭크 점수 총합을 뺀 것 ($1-S$)을 $1 \over {|V|}$ 로 공평하게 나눠 가지는 것이다. 이렇게 하면, 총량인 1도 맞출 수 있고, Dead End에서 나가는 간선도 만들어줄 수 있다.
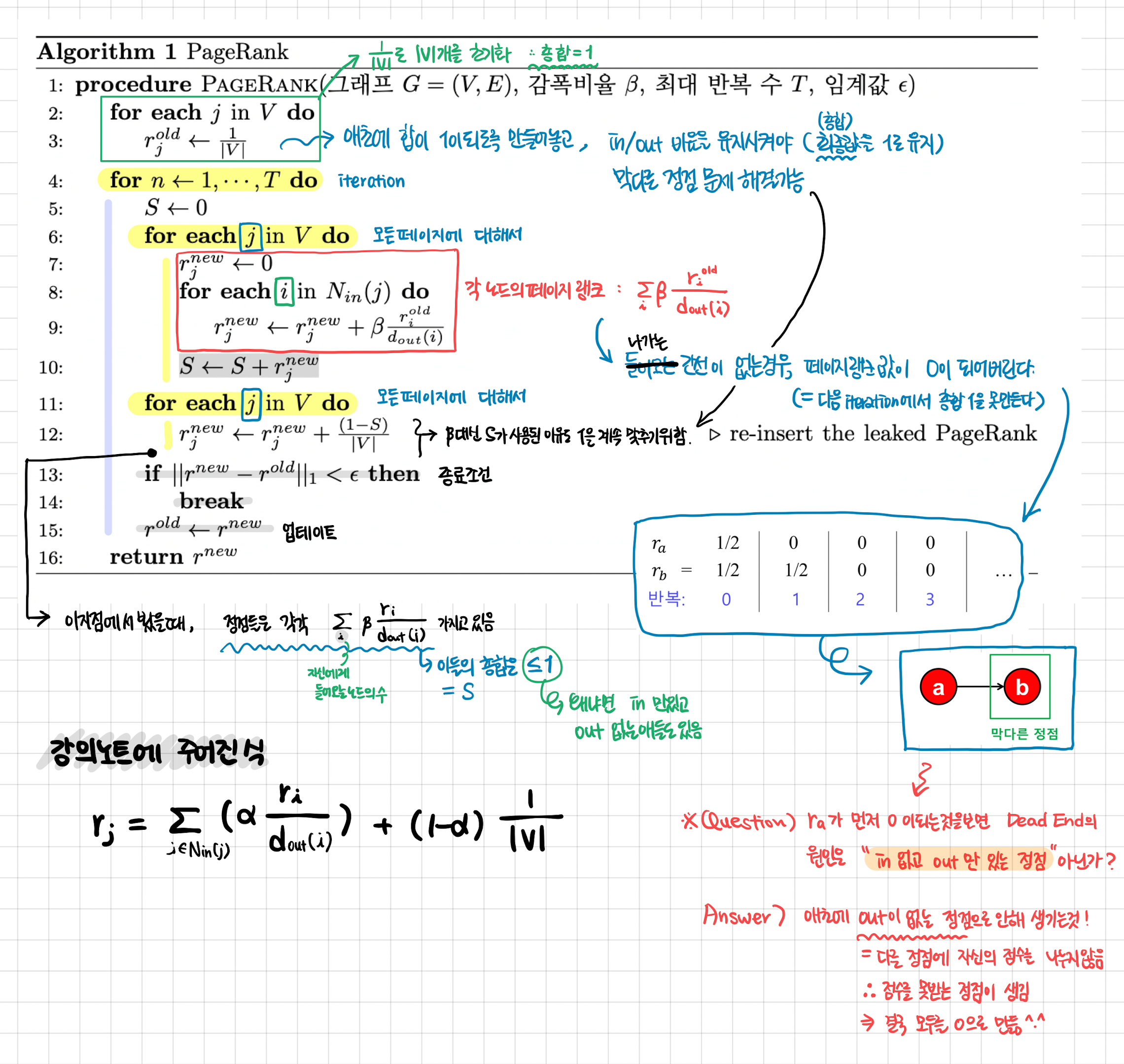
말로 설명하기 너무 어려워서 노트필기로 대체한다.